Financiële onafhankelijkheid

[Sibylle]

Uiteraard is 6% wel te doen, maar niet voor iedereen gedurende het hele leven
De meesten zullen ongeveer de beurzen volgen met hun beleggingswaarden, en met spaarrente ga je geen 6% halen gemiddeld ( 1% is more like it haha)

Er komt een moment dat je onderdeel bent van een crash/crisis oid. Daarnaast kom je misschien in een situatie waar je onverwachts veel geld moet neerleggen en je investeringen liquide moet maken, dat kost je rendement (en als het geld niet terugkomt vermogensdaling).

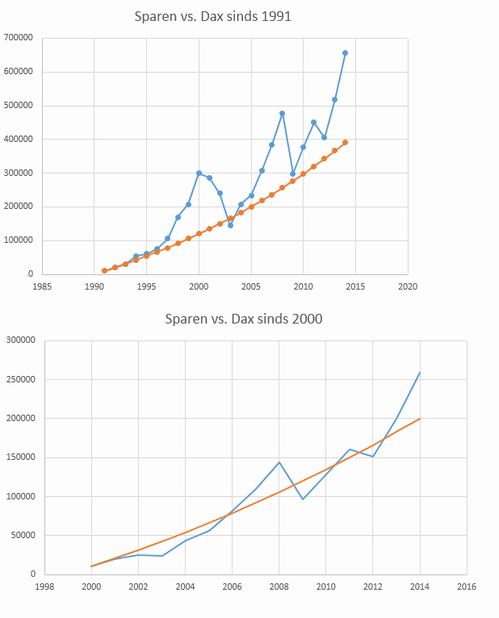
Ver vooruit kijken is erg lastig en meer iets van waarschijnlijkheidsverdelingen. Hier een tweetal plotjes die ik net gemaakt heb om eens in jullie op te nemen. Dit komt al iets meer in de buurt van hoe een FO berekening bekeken kan worden. Uiteraard is dit uiterst fictief, maar het geeft een idee.
Alle berekeningen in Excel, plotjes in Origin (maar Excel kan het ook perfect).

Ik heb:

1. Het jaarlijks rendement voor elk jaar random laten invullen (normaal verdeeld genomen met een gemiddelde van 5% en Std.Afw. van 1.5%). Dus: jaar1 =4.3% jaar2=7.6% jaar3=2.3% etc.
2. Twee random jaren op -12% gezet (alleen in het tweede geval)
3. Het vermogen (bij inleg van € 500 /maand) berekend over de jaren.
4. Opnieuw het jaarlijkse rendementen random laten invullen voor elk jaar
5. Opnieuw het vermogen (bij inleg van € 500 /maand) berekend over de jaren.
6. Repeat tig keer.

Daarna heb ik deze berekening nog 100 en 200 keer gedaan (n=100 en n=200) waarbij ik alleen gekeken heb naar wanneer €1M gehaald wordt. Die grafieken staan rechts.
Ik heb dus niet alle data van de rechter grafiek geplot in de linker (slechts een deel), want dan zou het een grote lijnenmassa worden met n=100 en 200.

[ Voor 47% gewijzigd door Sibylle op 16-07-2014 23:50 ]

[rr7r]

Arthas schreef op woensdag 16 juli 2014 @ 15:58:
[...]

Sparen is niks anders dan investeren, alleen doet iemand anders dat voor jou met jouw geld. (wel sparen via de bank,verzekering, etc. Niet het principe oude-sok-sparen, want dat levert helemaal niks op

Jij zet je spaargeld ter beschikking aan een bank.
Die bank leent het uit en maakt vervolgens rendement met jouw geld. Jij krijgt een percentage voor het ter beschikking stellen van je geld en de bank pakt de winst van het verschil tussen rente van de lening en van jouw spaargeld. Dat dit rendement nu zo laag is, is omdat er heel weinig risico aan verbonden is dat de bank jou niet terug kan betalen.

Je kunt er voor kiezen om de bank er tussen uit te halen en zelf die lening uit te geven, zoals kmf doet. Is dat dan een investering? Het verschil is dat je de tussenhandel eruit hebt gehaald en zelf het risico loopt dat er niet terugbetaald wordt. Daarvoor in de plaats krijg je een hoger rendement. Precies dat rendement wat de bank met jouw spaargeld gepakt heeft.

Oef. Het rendement is laag, omdat funding goedkoop en oneindig wordt aangeleverd (wel met onderpand alleen) door de ECB op dit moment. Met laag risico heeft dit alles niets te maken. Bovendien wordt spaargeld niet aangewend om uit te lenen. Bankkrediet ontstaat door wederzijdse schuldaanvaarding en het girale geld wat hierdoor "ontstaat" belandt vervolgens, wanneer niet chartaal opgenomen en nooit meer teruggestort, weer als banktegoed op de rechterzijde van de bankbalansen. Wanneer het betalingsverkeer zo verloopt dat er meer banktegoeden bij de ene bank dan bij de andere is, heeft de ene bank een fundingsprobleem. Dit risico dekken banken af met "spaargeld", d.w.z. rentevergoeding voor spaargeld in de hoop dat dit dode geld stabieler en voorspelbaarder is voor een bank.

Spaargeld is, behalve voor de spaarder zelf, nergens goed voor. Het is dood geld (het is niet in omloop), dient geen enkel doel (behalve funding, maar geld in omloop is net zo goed funding) en financiert vooral geen investeringen. Wanneer je spaargeld van de spaarder afpakt wordt daar niemand slechter van, behalve de spaarder zelf. Er zijn eerder argumenten die juist pleiten om dat nutteloze spaargeld af te pakken.

---

Over onderstaande ben ik wel benieuwd hoe medetweakers hier tegenaan kijken.

---

Banken hebben zich volgevreten met EMU staatsobligaties en verzekeraars doen dit al van oudsher. Wanneer EU-core-landen een financieringsprobleem krijgen en moeten afstempelen, dan gaan banken en verzekeraars bloeden, en mogelijk zodanig, dat ze failliet gaan. Combineer dat met de nieuwe bail-in regels en je realiseert je dat EMU staatsobligaties afstempelen = spaargeld afstempelen (boven de ton weliswaar, althans, zegt men). Beter is het dus om de spaarders maar direct te roven, dan spaar de banken en verzekeraars en bovendien zal je rente dalen, immers niets is dan veiliger dan diezelfde EMU staatsobligaties. Het depositogarantiestelsel is (tenzij er ergens een klein bankje omvalt) eigenlijk een fopspeen. De staat garandeert je spaargeld niet. Jij garandeert met je spaargeld de financierbaarheid van staatsobligaties.

[ Voor 24% gewijzigd door rr7r op 17-07-2014 02:53 ]

[Kapotlood]

@rr7r; ik ben 't met je eens dat spaargeld "dood geld" is. Maar is dat noodzakelijk slecht? Een hoop spaarders sparen liever geld dan dat ze het beleggen/investeren met de kans alles kwijt te zijn. Het is misschien voor iedereen (behalve de spaarder) dood geld, maar voor de spaarder zelf is het een veilig potje wat in principe nooit zomaar als sneeuw voor de zon verdwijnt… deze kans is er met beleggen e.d. namelijk wel (hoe klein of groot die kans ook is).

Dat je spaargeld dan alleen groeit wanneer je er zelf iets in stopt is daarna een heel ander verhaal… je maakt ten slotte geen/nauwelijks geld met geld met sparen Vroeger stopte men niet voor niets "spaargeld" letterlijk in een oude sok

Ik geloof overigens wel dat de komende 5-10 jaar de spaar- en beleggingswereld drastisch gaat veranderen. Zowel vanwege het feit dat banken steeds meer bekend staan als graaiers, vanwege de aanhoudende lage rente, en vanwege het feit dat beleggen ook steeds mákkelijker wordt. Wat dat betreft ben ik ervan overtuigd dat steeds meer mensen het heft in eigen handen nemen m.b.t. hun geld, en dat zal voor een aantal van deze mensen helpen meer inzicht te krijgen in FO en de mogelijkheden ervan.

Voor mij zijn de bovenstaande redenen om op z'n minst een déél van het geld wat ik jaarlijks over hou, te investeren in indexbeleggen. Heb gister notabene een account aangemaakt bij Ohpen met een klein startbedrag om m'n voetjes nat te krijgen… raak ik daar bekend mee en voelt 't goed, dan hoop ik zo'n 30-50% van m'n te sparen geld daarin te kunnen beleggen.

[Aliene]

joramoudenaarde schreef op donderdag 17 juli 2014 @ 08:10:

Voor mij zijn de bovenstaande redenen om op z'n minst een déél van het geld wat ik jaarlijks over hou, te investeren in indexbeleggen. Heb gister notabene een account aangemaakt bij Ohpen met een klein startbedrag om m'n voetjes nat te krijgen… raak ik daar bekend mee en voelt 't goed, dan hoop ik zo'n 30-50% van m'n te sparen geld daarin te kunnen beleggen.

Mag ik vragen waarom je voor Ohpen hebt gekozen?

[demichel]

Aliene schreef op woensdag 16 juli 2014 @ 09:19:
[...]
Ik denk ook dat heel veel mensen op kleding kunnen bezuinigen. Ik heb dit jaar zelf uitgeprobeerd om een jaar helemaal geen kleding te kopen, gewoon om te zien of ik het vol zou houden. Dat is niet gelukt (wel 6 maanden, maar laatst zo'n 70 euro uitgegeven), maar je beseft je wel dat je helemaal niet zoveel nodig hebt. Bovendien scheelde het bij mij veel vrije tijd en ergernis (op zaterdag door de overvolle stad heen sjouwen...).

Vind ik nu eens heel erg makkelijk. Ik heb dan ook een ongelofelijke rothekel aan kleding passen en kopen. Een tiental jaar geleden in een kwartier tijd vijftien hemdjes met korte mouwen gekocht in een supermarkt in Singapore, een tiental jeans in een discount store in Hong Kong en een tijd geleden een tiental Riverwood hemden aan 15€ per stuk bij een gigantische reclame in Lille in Frankrijk en dat is het dan ook. De afgelopen vijf jaar of zo staan uitgaven aan kledij voor mezelf op 0€.

[MrAcid]

Ik wil wat geld weg gaan zitten een EFT's. Ik zit er zelf aan te denken om dit via ING te doen, die hebben daar volgens mij tegenwoordig best wel prima tarieven voor. Het hierboven genoemde Ohpen lijkt me vrij duur als je maandelijks wilt inleggen, aangezien je 0,5% transactiekosten betaald. Dat is best wel fors voor trackers?

Ik zit zelf aan de Think EFTs te denken overigens. Lage TER en geen dividendlekkage. Hebben meer mensen daar geld in zitten hier? Zo niet, welke hebben jullie zelf? En waarom?

edit:
Nog even goed gezocht in het topic, en dan is deze discussie al vaker gevoerd - ik kan alleen geen duidelijk antwoorden vinden over wat mensen zelf gedaan hebben.

Dit is een veel aangehaalde link die denk ik interessant is voor iedereen om te lezen:
http://econowiser.wordpress.com/2013/11/29/1139/

Daar kun je in elk geval zien dat de Think EFT's niet zo interessant zijn als ze in eerste instantie ogen: te weinig spreiding (250 stuks tegenover 1600 in Vanguards EFT's). Conclusie van de schrijver daar is om te investeren in Vanguard via BinckBank in NL, en dan de transactiekosten maar voor lief te nemen.

Daarbij moet je er rekening mee houden dat je eigenlijk het beste minimaal €3500 kunt inleggen per keer ivm minimale transactiekosten van €10.

LASTIG!

[ Voor 65% gewijzigd door MrAcid op 17-07-2014 09:32 . Reden: Beetje beter gezocht... ]

[Kapotlood]

@Aliene; eigenlijk om een aantal, voor mij belangrijke, redenen:
- Er was geen minimum bedrag wat je "moet" inleggen.
- De instap was laag omdat je 't zowel tot in de puntjes zelf kan regelen, óf alles automatisch kan laten beleggen.
- Het overzicht van de website, de portefeuille en de fondsen heel netjes en duidelijk weergegeven zijn.
- De kosten van deze portefeuille waren ook lager dan anderen die ik heb gevonden.
- Het is een nieuw bedrijf die, voor zover ik alles heb terug kunnen lezen, een hoop mooie reviews heeft gekregen.
- Het geld wat ik stort staat nooit vast: ik zou morgen de boel weer kunnen opnemen zonder boete (alleen een 0,5% transactiekosten over het bedrag).

Ohpen geeft overigens zelf wel aan dat als je heel actief wil beleggen of "buitengewoon" risico wil nemen, dat je niet bij hun moet zijn. Dat was voor mij ook een extra reden… ik ben nu voor het eerst echt bezig met beleggen, dus de lage instap e.d. waren voor mij reden genoeg om het bij Ohpen eens te proberen. Baat het niet dan schaad het nauwelijks

[Aliene]

@Joram
Bedankt, dat is duidelijk. Ik ben zelf ook net begonnen, en wil vooral niet te veel hoeven te doen. Ik heb voor meesmand gekozen omdat de kosten laag zijn. Maar je maakt in principe elke maand hetzelfde bedrag over. Als je dat wilt wijzigen moet je dat ruim van te voren doen (volgens mij 1,5 week ofzo), dus daardoor is het wel wat beperkter.

[Kapotlood]

Ik heb ook naar Meesman zitten kijken, maar ik kon op hun site geen tool vinden om een klein beetje de indruk te krijgen hoe het verloop in geld zit met beleggen, en wat ik eventueel moet/kan doen. (eenmalige inzet, maandelijkse inzet e.d.). Ik miste ook een beetje (voor 'n beginner als mij ten minste) een transparant overzicht in de mogelijkheden e.d., dus dat was voor mij de doorslag

[_l_Arjan_l_]

MrAcid schreef op donderdag 17 juli 2014 @ 08:36:
Ik wil wat geld weg gaan zitten een EFT's. Ik zit er zelf aan te denken om dit via ING te doen, die hebben daar volgens mij tegenwoordig best wel prima tarieven voor. Het hierboven genoemde Ohpen lijkt me vrij duur als je maandelijks wilt inleggen, aangezien je 0,5% transactiekosten betaald. Dat is best wel fors voor trackers?

Bij ING heb je vaste kosten per kwartaal (4 euro) en een service fee per jaar van 0.24%. Transactiekosten voor belegginsfondsen zijn er niet.
Transactiekosten van losse aandelen/obligaties zijn ook erg laag (4 euro plus een klein percentage).

Voor kleine bedragen is de ING volgens mij best gunstig qua tarieven. Voor grotere bedragen niet vanwege die service fee van 0.24%.

[MrAcid]

Dank voor je input. Ik ben nu even een Excel sheet aan het maken waar ik al dat soort kosten tegen elkaar kan uitzetten.

[Mr_Blobby]

Aliene schreef op donderdag 17 juli 2014 @ 09:45:
@Joram
Bedankt, dat is duidelijk. Ik ben zelf ook net begonnen, en wil vooral niet te veel hoeven te doen. Ik heb voor meesmand gekozen omdat de kosten laag zijn. Maar je maakt in principe elke maand hetzelfde bedrag over. Als je dat wilt wijzigen moet je dat ruim van te voren doen (volgens mij 1,5 week ofzo), dus daardoor is het wel wat beperkter.

Ik ben begin dit jaar bij Meesman begonnen.
De voordelen van Meesman ten opzichte van Ophen is:
Lagere transactiekosten (0,25% i.p.v. 0,50%)
Ze hebben een wereldwijd fonds dat een standaard index volgt.
Ophen biedt regionale fondsen die zijn opgebouwd uit een zeer beperkt aantal aandelen (bijv. 50 voor Noord Amerika). Meesman wereldwijd volgt de MSCI world index die uit 1600 verschillende bedrijven bestaat.
Ik kan niet ontdekken welke benchmark of index Ophen hanteert.
Meesman heeft met hun Wereldwijde fonds geen dividendlek.
Een brede spreiding is in mijn optiek heel belangrijk en 50 bedrijven is veel te weinig.

[Avinator88]

Naar mijn idee zijn juist de beheerskosten de killer. Die zijn standaard 0.5%, dit kan lager bij Meesman (kan ook hoger, hangt van je portfolio af). Ik vind het moeilijk om een duidelijk goed onderbouwde keuze maken echter. Ik zie dat ik voor een mooie spreiding 2 rekeningen nodig heb:
1. Maandelijks inleg in indexfondsen, met dus lage beheerskosten
2. High dividend stock picking, met lage transactiekosten

Die 2 rekeningen vinden in NL is nog een flinke klus die voor de boeg staat.

Plus: http://www.telegraaf.nl/d...t_vermogensbeheer___.html
Is het denk ik nu Binckbank.

[Verwijderd]

Avinator88 schreef op donderdag 17 juli 2014 @ 10:22:
Naar mijn idee zijn juist de beheerskosten de killer. Die zijn standaard 0.5%, dit kan lager bij Meesman (kan ook hoger, hangt van je portfolio af). Ik vind het moeilijk om een duidelijk goed onderbouwde keuze maken echter. Ik zie dat ik voor een mooie spreiding 2 rekeningen nodig heb:
1. Maandelijks inleg in indexfondsen, met dus lage beheerskosten
2. High dividend stock picking, met lage transactiekosten

Die 2 rekeningen vinden in NL is nog een flinke klus die voor de boeg staat.

Plus: http://www.telegraaf.nl/d...t_vermogensbeheer___.html
Is het denk ik nu Binckbank.

Ikzelf doe het bij Degiro.nl Daar heb je voor een grote selectie EFT's geen transactiekosten. Dat weegt naar mijn mening ruim op tegen het "uitleen" risico.

[MrAcid]

Verwijderd schreef op donderdag 17 juli 2014 @ 10:35:
[...]


Ikzelf doe het bij Degiro.nl Daar heb je voor een grote selectie EFT's geen transactiekosten. Dat weegt naar mijn mening ruim op tegen het "uitleen" risico.

Maar welke EFT's zijn dat? Daar heb ik nog niks over kunnen vinden.

[hv08]

Staan in het document center:
https://www.degiro.nl/dat...Trackers_Kernselectie.pdf

https://www.degiro.nl/dat...sfondsen_Kernselectie.pdf

[Kapotlood]

Beginnen met beleggen is (vind ik) ook erg lastig. De kosten, de fondsen, de uitleg… alles lijkt nét even anders verteld en bekostigd te worden. Voor een beginner is het behoorlijk lastig om houvast te krijgen in hoe je dit goed kan vergelijken.

Bij Meesman zijn de kosten misschien over de hele linie lager, maar ik vond hun site en uitleg nét even boven dat van een beginner vallen. Dat ze een veel gespreider portfolio hebben is nu ik dat zo lees wel beter dan dat van Ohpen, maar ik blijf voor het komende jaar bij Ohpen vooral om een béétje te leren beleggen voordat ik met lagere kosten én met minder inzicht/overzichtelijkheid bij een ander ga zitten

[Terpen Tijn]

MrAcid schreef op donderdag 17 juli 2014 @ 08:36:
Ik wil wat geld weg gaan zitten een EFT's. Ik zit er zelf aan te denken om dit via ING te doen, die hebben daar volgens mij tegenwoordig best wel prima tarieven voor. Het hierboven genoemde Ohpen lijkt me vrij duur als je maandelijks wilt inleggen, aangezien je 0,5% transactiekosten betaald. Dat is best wel fors voor trackers?

Ik zit zelf aan de Think EFTs te denken overigens. Lage TER en geen dividendlekkage. Hebben meer mensen daar geld in zitten hier? Zo niet, welke hebben jullie zelf? En waarom?

edit:
Nog even goed gezocht in het topic, en dan is deze discussie al vaker gevoerd - ik kan alleen geen duidelijk antwoorden vinden over wat mensen zelf gedaan hebben.

Dit is een veel aangehaalde link die denk ik interessant is voor iedereen om te lezen:
http://econowiser.wordpress.com/2013/11/29/1139/

Daar kun je in elk geval zien dat de Think EFT's niet zo interessant zijn als ze in eerste instantie ogen: te weinig spreiding (250 stuks tegenover 1600 in Vanguards EFT's). Conclusie van de schrijver daar is om te investeren in Vanguard via BinckBank in NL, en dan de transactiekosten maar voor lief te nemen.

Daarbij moet je er rekening mee houden dat je eigenlijk het beste minimaal €3500 kunt inleggen per keer ivm minimale transactiekosten van €10.

LASTIG!

Is er bewijs voor dat het spreiden over 1600 van dergelijke fondsen (i.e., global, developed markets, etc) in plaats van 250 een betekenisvol voordeel biedt? Ik zou denken dat je de variantie wat verder reduceert, maar omdat de afname daarvan per toegevoegd fonds steeds verder krimpt lijkt me het effect ervan niet supergroot. Bij een crisis heb je dan iets minder verlies, maar bij groei mogelijk ook minder winst. Is dat zo aantrekkelijk?

[MrAcid]

Dat weet ik niet, ik heb het niet paraat in elk geval. Theoretisch is het uiteraard mogelijk dat die twee elkaar positief of negatief zullen ontlopen. Dat weet ik niet.

Maar van die index gebaseerd op 1600 aandelen is een geschiedenis sinds 1969 terug te vinden om de prestaties te beoordelen. Van die 250 niet.

Dank voor de link naar De Giro met de EFT's zonder transactiekosten! Dat wordt voor nu mijn go-to voor aankoop.

[Cloud]

Beleggen in dat soort fondsen doe je natuurlijk niet voor de grote winst maar voor de veiligheid. Dus inderdaad, meer spreiding heeft de voorkeur lijkt mij.

Zelf ben ik hier ook naar aan het kijken en had zelf De Giro er ook voor op het oog. Ik kon alleen geen lijst met fondsen vinden, dank voor die lijst hv08!

[hv08]

Ze hebben trouwens ook nog obligaties zonder kosten zag ik net:

https://www.degiro.nl/dat...ligaties_Kernselectie.pdf

[Aliene]

joramoudenaarde schreef op donderdag 17 juli 2014 @ 10:49:
Beginnen met beleggen is (vind ik) ook erg lastig. De kosten, de fondsen, de uitleg… alles lijkt nét even anders verteld en bekostigd te worden. Voor een beginner is het behoorlijk lastig om houvast te krijgen in hoe je dit goed kan vergelijken.

Bij Meesman zijn de kosten misschien over de hele linie lager, maar ik vond hun site en uitleg nét even boven dat van een beginner vallen. Dat ze een veel gespreider portfolio hebben is nu ik dat zo lees wel beter dan dat van Ohpen, maar ik blijf voor het komende jaar bij Ohpen vooral om een béétje te leren beleggen voordat ik met lagere kosten én met minder inzicht/overzichtelijkheid bij een ander ga zitten

Als je geinteresseerd bent in index beleggen, is wellicht het boek 'de schitterende eenvoud van indexbeleggen' leuk om te lezen. Dit is echt heel begrijpbaar geschreven. Ik had m bij de bieb geleend, is het ook nog gratis .
Verder, als je iets niet snapt en meesman mailt krijg je binnen een dag duidelijk antwoord. (Ik probeer je niet over te halen naar een ander te gaan hoor, just fyi)

[ Voor 0% gewijzigd door Aliene op 17-07-2014 11:11 . Reden: foute boektitel ]

[Bonsaiboom]

Voor DeGiro: Ik heb begrepen dat in de voorwaarden daar staat dat zij de stukken die jij koopt mogen uitlenen, er een vergoeding voor krijgen, en dat jij het risico erover loopt. Dat is nogal een grote hidden cost, waardoor ze zaken goedkoper aanbieden dan dat het daadwerkelijk is. Meesman doet dat niet. die koopt de stukken en houdt ze apart voor je. Voor niets gaat de zon op, geldt zeker in obligatie en aandelenland.

De belangrijke link naar econowiser blog is al gedaan zie ik, en sommigen kiezen inderdaad bewust voor dit risico. Ik weet niet hoe dat is bij Ohpen. Ikzelf zou liever wat hogere kosten accepteren, en dat ik daarmee helder heb wat ik in mijn bezit heb, wat ik iemand betaal voor de diensten die ze mij leveren en wat ik kan verwachten, in plaats van in een potentieel juridisch complexe nachtmerrie terecht te komen.

[Mr_Blobby]

Bij De Giro hebben ze wel een spread (aankoopprijs is hoger dan verkoopprijs).
Daarin zit bijv. 0,10% wanneer je iets koop wat in dollars staat genoteerd.
Dus je betaalt wel een soort transactiekosten, alleen zijn ze verborgen.

[rr7r]

VEB Brokeronderzoek 2014.

[MrAcid]

Dat klopt inderdaad, daar moet je goed op letten!

Voorbeeld van het Vanguard Total World Stock Index Fund... Bied 61,510 - Laat 72,000(!)

[Kapotlood]

@Aliene; bedankt! Ik hou van Jip en Janneke taal, dus ik duik even in dat boek

[PromWarMachine]

Sibylle schreef op woensdag 16 juli 2014 @ 23:13:
Uiteraard is 6% wel te doen, maar niet voor iedereen gedurende het hele leven
De meesten zullen ongeveer de beurzen volgen met hun beleggingswaarden, en met spaarrente ga je geen 6% halen gemiddeld ( 1% is more like it haha)

Er komt een moment dat je onderdeel bent van een crash/crisis oid. Daarnaast kom je misschien in een situatie waar je onverwachts veel geld moet neerleggen en je investeringen liquide moet maken, dat kost je rendement (en als het geld niet terugkomt vermogensdaling).

Ver vooruit kijken is erg lastig en meer iets van waarschijnlijkheidsverdelingen. Hier een tweetal plotjes die ik net gemaakt heb om eens in jullie op te nemen. Dit komt al iets meer in de buurt van hoe een FO berekening bekeken kan worden. Uiteraard is dit uiterst fictief, maar het geeft een idee.
Alle berekeningen in Excel, plotjes in Origin (maar Excel kan het ook perfect).

[..]

Dank voor je berekening!
Dit ziet er inderdaad wat minder optimistisch, maar wat meer realistisch uit

Is hij makkelijk opnieuw uit te rekenen voor €750 & €1000 per maand?
Als ik 48 spaarjaren nodig heb, ben ik alsnog 78, dan hoop ik eigenlijk al een jaar of 15 met pensioen te zijn.._{als ik het uberhaupt haal uiteraard..}

[hv08]

joramoudenaarde schreef op donderdag 17 juli 2014 @ 11:22:
@Aliene; bedankt! Ik hou van Jip en Janneke taal, dus ik duik even in dat boek

Hou even in het achterhoofd dat het boek is geschreven door de mensen achter Meesman

[Aliene]

hv08 schreef op donderdag 17 juli 2014 @ 11:26:
[...]


Hou even in het achterhoofd dat het boek is geschreven door de mensen achter Meesman

Ja klopt, maar het gaat vooral over indexbeleggen in het algemeen. Niet over de verschillende aanbieders als ik het me goed herinner.

[Burlok86]

MrAcid schreef op donderdag 17 juli 2014 @ 08:36:
Daar kun je in elk geval zien dat de Think EFT's niet zo interessant zijn als ze in eerste instantie ogen: te weinig spreiding (250 stuks tegenover 1600 in Vanguards EFT's). Conclusie van de schrijver daar is om te investeren in Vanguard via BinckBank in NL, en dan de transactiekosten maar voor lief te nemen.

Daarbij moet je er rekening mee houden dat je eigenlijk het beste minimaal €3500 kunt inleggen per keer ivm minimale transactiekosten van €10.

LASTIG!

Bij ING hebben ze ook varia Vanguard ETF's, kost jaarlijks €16 waarbij ETF's geen transactiekosten hebben.
Daar ben ik zelf begonnen maandelijks geld in te storten, werkt best handig bij ING.

*Hier komen inderdaad de variabele kosten nog bij;
Tot en met €75.000 0,24%
Over het meerdere t/m €500.000 0,12%
Over het meerdere t/m €2.500.000 0,06%

[ Voor 10% gewijzigd door Burlok86 op 17-07-2014 12:13 ]

[Avinator88]

Burlok86 schreef op donderdag 17 juli 2014 @ 12:01:
[...]


Bij ING hebben ze ook varia Vanguard ETF's, kost jaarlijks €16 waarbij ETF's geen transactiekosten hebben.
Daar ben ik zelf begonnen maandelijks geld in te storten, werkt best handig bij ING.

Maar bij ING heb je toch ook beheerskosten?

Edit:
Klopt idd: https://www.ing.nl/partic...rieven/tarieven-beleggen/
Ze noemen het een servicefee van 0.24% en dit komt bovenop de beheerskosten van de ETF. Een soort bewaarloon dus, en daarbij betaal je dus ook de 16e per jaar.

[ Voor 25% gewijzigd door Avinator88 op 17-07-2014 12:10 ]

[DeZaag]

Avinator88 schreef op donderdag 17 juli 2014 @ 12:06:
[...]


Maar bij ING heb je toch ook beheerskosten?

Klopt, 0,24%. Bij lagere bedragen interessant.

[Mr_Blobby]

Het hangt natuurlijk af van de percentages en hoeveel je handel, maar in het algemeen zijn jaarlijkse (beheer)kosten veel schadelijker voor het rendement op termijn, dan eenmalige (transactie)kosten.

Naast de blog van Econowiser, vond ik de site van Erica Verdegaal ook leerzaam.
Bijvoorbeeld: Drie keer wegwijs in indexbeleggen en Indexbeleggen, blijf alert op kosten

[ Voor 46% gewijzigd door Mr_Blobby op 17-07-2014 12:24 ]

[DeZaag]

Mr_Blobby schreef op donderdag 17 juli 2014 @ 12:19:
Het hangt natuurlijk af van de percentages en hoeveel je handel, maar in het algemeen zijn jaarlijkse (beheer)kosten veel schadelijker voor het rendement op termijn, dan eenmalige (transactie)kosten.

Eens.

Bij het maandelijks lage bedragen in meerdere ETF's inleggen middels het DCA-principe is de ING interessant.

Bij het 1x per jaar aanschaffen van een dividend aristocrat is de ING absoluut niet interessant.

Maar goed, deze discussie is mijns inziens meer geschikt voor het Beleggen topic.

[MrAcid]

Ik heb een sheetje in elkaar geknutseld waarmee je het kunt berekenen. Feel free to use:
Nieuwe versie

Heb niet al teveel verklaringen opgenomen dus het is mogelijk even puzzelen voor je doorhebt hoe hij ingevuld moet worden. De "roze kleurige" cellen moet je zelf invullen.

Periodieke inleg = maandelijks
Servicefee = jaarlijkse fee (bewaarloon - dus niet de TER)

De vermogensopbouw wordt niet helemaal netjes berekend (per jaar, niet per maand) waardoor de kosten niet 100% kloppen, maar het geeft een goed genoeg beeld voor mijn eigen gebruik.

[ Voor 12% gewijzigd door MrAcid op 18-07-2014 09:55 ]

[kmf]

Let ook op het gemak he.

Wordt bij een inleg direct "aangekocht" of wordt het (zoals bij BrandNewDay) al het geld opgespaard en op 1 aankoopmoment aangekocht.

[Aliene]

MrAcid schreef op donderdag 17 juli 2014 @ 12:26:
Ik heb een sheetje in elkaar geknutseld waarmee je het kunt berekenen. Feel free to use:
https://dl.dropboxusercon...illende%20aanbieders.xlsx

Heb niet al teveel verklaringen opgenomen dus het is mogelijk even puzzelen voor je doorhebt hoe hij ingevuld moet worden. De "roze kleurige" cellen moet je zelf invullen.

Periodieke inleg = maandelijks
Servicefee = jaarlijkse fee

De vermogensopbouw wordt niet helemaal netjes berekend (per jaar, niet per maand) waardoor de kosten niet 100% kloppen, maar het geeft een goed genoeg beeld voor mijn eigen gebruik.

Super! Bedankt! Ga er dit weekend eens mee spelen.

[Bonsaiboom]

DeZaag schreef op donderdag 17 juli 2014 @ 12:24:
[...]


Eens.

Bij het maandelijks lage bedragen in meerdere ETF's inleggen middels het DCA-principe is de ING interessant.

Bij het 1x per jaar aanschaffen van een dividend aristocrat is de ING absoluut niet interessant.

Maar goed, deze discussie is mijns inziens meer geschikt voor het Beleggen topic.

Mijns inziens past hij hier prima. Belegtactieken passen in FO, en de meesten hier willen eigenlijk een no-fuss, prima tactiek. Die bespreek je hier. Het beleggen topic gaat vaak al over stockpicking e.d. en manieren waarop je de beurs verslaat in plaats hem volgt. Een dergelijke passieve benadering tot beleggen past volgens mij hier goed in dit topic.

[Verwijderd]

MrAcid schreef op donderdag 17 juli 2014 @ 12:26:
Ik heb een sheetje in elkaar geknutseld waarmee je het kunt berekenen. Feel free to use:
https://dl.dropboxusercon...illende%20aanbieders.xlsx

Heb niet al teveel verklaringen opgenomen dus het is mogelijk even puzzelen voor je doorhebt hoe hij ingevuld moet worden. De "roze kleurige" cellen moet je zelf invullen.

Periodieke inleg = maandelijks
Servicefee = jaarlijkse fee

De vermogensopbouw wordt niet helemaal netjes berekend (per jaar, niet per maand) waardoor de kosten niet 100% kloppen, maar het geeft een goed genoeg beeld voor mijn eigen gebruik.

Dank. En verrassend! Bij lage inleg is ING dus het meest voordelig.
En Binck is dan juist helemaal niet voordelig. Grappig, omdat Binck zich destijds op de markt heeft gebracht als prijsvechter en ook daadwerkelijk veel goedkoper was dan ING.

[zomertje]

Ik zit bij Binck Fundcoach, op zich ook niet heel goedkoop. Maar ben heel tevreden over de site en heb dankzij dit topic mn eerste ETF aangekocht Je kan er maandelijks aankopen zonder kosten, dat is dan weer wel voordelig.

[kmf]

Verwijderd schreef op donderdag 17 juli 2014 @ 13:02:
[...]


Dank. En verrassend! Bij lage inleg is ING dus het meest voordelig.
En Binck is dan juist helemaal niet voordelig. Grappig, omdat Binck zich destijds op de markt heeft gebracht als prijsvechter en ook daadwerkelijk veel goedkoper was dan ING.

Hoe heb je het ingevuld dan, want wat ik ook invul. BrandNewDay (zelf toegevoegd aan het document) met 0,50% transactiekosten en 0,59% beheerkosten blijft het goedkoopste.

zomertje schreef op donderdag 17 juli 2014 @ 13:04:
Ik zit bij Binck Fundcoach, op zich ook niet heel goedkoop. Maar ben heel tevreden over de site en heb dankzij dit topic mn eerste ETF aangekocht Je kan er maandelijks aankopen zonder kosten, dat is dan weer wel voordelig.

Ik zit op Binck Basic. Maar dat komt omdat ik al veel eerder ETFs daar heb gekocht. Deze is goedkoop als je in 1x een groot bedrag (1500+) inlegt. Dus daar hou ik het biij.

[ Voor 32% gewijzigd door kmf op 17-07-2014 13:09 ]

[hv08]

Als je periodiek inlegt moet je binck fundcoach gebruiken. Die kost 0.15% over portefeuillewaarde (minimaal 60 per jaar), dat scheelt nogal wat

En als je toch bezig bent, de ter is ook nog wel belangrijk. Meesman kan goedkoper qua aanschaf zijn, maar misschien is de ter hoger dan bijvoorbeeld BND ter.

Het is toch iets lastiger

[MrAcid]

Let even op dat die servicefee in mijn Excelsheet bedoeld is als bewaarloon, niet als TER! Dit omdat de TER altijd al verwerkt zit in de koers van de tracker (en verschilt per tracker).

Dit is puur een vergelijking van aanbieders waar je dan periodiek EFT's zou kopen, waarbij dat een "generieke EFT" is die je bij meerdere aanbieders aan zou kunnen schaffen.

[ Voor 60% gewijzigd door MrAcid op 17-07-2014 13:11 ]

[kmf]

hv08 schreef op donderdag 17 juli 2014 @ 13:09:
Als je periodiek inlegt moet je binck fundcoach gebruiken. Die kost 0.15% over portefeuillewaarde (minimaal 60 per jaar), dat scheelt nogal wat

En als je toch bezig bent, de ter is ook nog wel belangrijk. Meesman kan goedkoper qua aanschaf zijn, maar misschien is de ter hoger dan bijvoorbeeld BND ter.

Het is toch iets lastiger

Je hoeft het niet bij 1 broker houden. Ik heb bv BinckBank EN BND.
BND doe ik m'n periodieke inleg.

Binck voor de grotere bulkaankopen die ik 1x per jaar doet. Voordeel van Binck is dat je veel meer keuzemogelijkheden hebt in ETFs.

[Coldcat]

Het nadeel can de ING is dat je daar dan ook je bankaccount moet hebben. Anders komen die kosten er bovenop.

Volgens mij ontloopt de rabobank dan niet heel veel.

[Schinnen-groen]

Poe, poe, pijn aan de ogen van het bijlezen.

Ik begrijp dus dat voor FO je flink in de beleggingen moet gaan

Mag ik dan al een 25 jaar lange ervaringsdeskundige met aandelen beleggen zeggen dat dit niet de "gouden weg is".

Dat is schulden afbouwen, vaste lasten reduceren en een redelijke spaarrekening (of rekeningen), wel.
Ook een andere kijk op je bestedingspatroon, zoal velen al hebben, scheelt enorm veel.


Het begint een beetje op een beleggingssite te lijken....

[MrAcid]

Wat ga je doen met al het geld dat je bespaart/niet uitgeeft dan?

[Verwijderd]

Je zult dat geld uiteindelijk voor je moeten laten werken maar ik zie het pad naar FO als wielrennen. Ga bijvoorbeeld niet €6000 uitgeven aan een fiets van koolstof die 2kg lichter is dan je huidige als je zelf nog 15kg op je buik hebt hangen ;-)

Zorg dat je eerst in "FO conditie" bent (dus min mogelijk schulden en overbodige uitgaven" en ga dan pas investeren, liefst differentiatie toepassen dus niet alles beleggen maar ook sparen/eigen bedrijf/handeltje in iets enz...

[Cloud]

Schinnen-groen schreef op donderdag 17 juli 2014 @ 13:27:
[...]
Dat is schulden afbouwen, vaste lasten reduceren en een redelijke spaarrekening (of rekeningen), wel.
Ook een andere kijk op je bestedingspatroon, zoal velen al hebben, scheelt enorm veel.
[...]

Je begint uiteraard met die zaken maar als je uiteindelijk niet meer schulden kunt afbouwen, niet meer lasten kunt verlichten en al een flinke spaarrekening hebt dan kun je een deel ook gaan beleggen in de meest veilige beleggingsvormen. Uiteraard moet je de risico's ervan accepteren maar je kunt je rendement er wel mee verbeteren En je hebt ook 'passieve' inkomsten nodig om uiteindelijk op FO te komen lijkt me.

[Schinnen-groen]

Cloud schreef op donderdag 17 juli 2014 @ 13:50:
[...]

Je begint uiteraard met die zaken maar als je uiteindelijk niet meer schulden kunt afbouwen, niet meer lasten kunt verlichten en al een flinke spaarrekening hebt dan kun je een deel ook gaan beleggen in de meest veilige beleggingsvormen. Uiteraard moet je de risico's ervan accepteren maar je kunt je rendement er wel mee verbeteren En je hebt ook 'passieve' inkomsten nodig om uiteindelijk op FO te komen lijkt me.

Maar dan ben je al ver: huis is afbetaald, energieverbruik verwaarloosbaar, geen schulden meer.
Als je daarna op een punt komt dat je meer geld hebt dan je nodig hebt om tot je dood lekker te leven, dan kan je met het resterend bedrag gaan gokken. Beleggen is namelijk gokken. beleggen heeft tegenwoordig heel weinig meer te maken met koers/winst verhoudingen en financiële jaaroverzichten, maar meer met het idee dat er altijd verdiend kan worden. Dat die verdienste betaalt worden met het verlies van anderen (en die andere kan jij ook zijn) wordt maar even voor het gemak vergeten.

Elke belegging is een gok en als je dat, met de kennis van de afgelopen 10 jaar, nog niet hebt begrepen dan wordt het tijd om je toch eens achter de oren te krabben voordat je aan beleggen wilt beginnen.

Gokken moet je doen met geld dat je toch niet nodig hebt.

[Kapotlood]

@Schinnen-groen; beleggen is toch niet echt zo negatief qua inkomstenvergaring? Ik bedoel, je kan altijd een negatief moment hebben in de tijd dat je belegt, maar winst wordt niet (altijd) betaald door het verlies van een ander dacht ik… het zijn ook investeringen die in bedrijven worden gedaan die op hun beurt met de gemaakte winst (door de service/producten die ze aanbieden) weer uitkeren als dividend (als ik 't goed heb begrepen).

[rr7r]

Schinnen-groen schreef op donderdag 17 juli 2014 @ 14:52:
[...]

Dat die verdienste betaalt worden met het verlies van anderen (en die andere kan jij ook zijn) wordt maar even voor het gemak vergeten.

Het is ook niet helemaal waar namelijk.

Voorbeeld:
Een bedrijf geeft 10 aandelen uit aan 10 beleggers á € 10,-
De daarop volgende kwartaalresultaten van het bedrijf zijn boven verwachting van een elfde belegger en is bereid € 15 te betalen en plaatst een order van 1 aandeel in het lege orderboek. Belegger nummer 1 wil echter, om wat voor reden ook, van haar aandeel af. Zij ziet in het orderboek een biedkoers van € 15 en biedt haar aandeel voor dit bedrag aan (bestens order). De transactie vindt plaatst. De koers stijgt n.a.v. dit gebeuren naar € 15,-

In dit voorbeeld hebben 10 beleggers € 5,- gewonnen en staat 1 belegger op break/even. Er zijn geen verliezers.

[Schinnen-groen]

joramoudenaarde schreef op donderdag 17 juli 2014 @ 15:04:
@Schinnen-groen; beleggen is toch niet echt zo negatief qua inkomstenvergaring? Ik bedoel, je kan altijd een negatief moment hebben in de tijd dat je belegt, maar winst wordt niet (altijd) betaald door het verlies van een ander dacht ik… het zijn ook investeringen die in bedrijven worden gedaan die op hun beurt met de gemaakte winst (door de service/producten die ze aanbieden) weer uitkeren als dividend (als ik 't goed heb begrepen).

Een aandelenkoers is iets anders dan divident. Een aandelenkoers is tegenwoordig voor het grootste gedeelte bepaald door "gevoel'. Bij Binck bijvoorbeeld wordt zelfs bij verschillende aandelen aangegeven hoe het aandeel wordt genoemd in de social media: positief of negatief. Dat heeft weinig meer te maken met de echte waarde van een bedrijf (en dus de waarde van het aandeel), maar alles met sentiment.
En je weet hopelijk hoe sentiment werkt...

Nogmaals: als je het geld prima kan missen, doen!! Maar heb je nog een hypo, of zo: aflossen.

Just my two cents.

[Cloud]

Schinnen-groen schreef op donderdag 17 juli 2014 @ 14:52:
[...]
Gokken moet je doen met geld dat je toch niet nodig hebt.

Absoluut. Beleggen moet je pas aan beginnen nadat je een goede buffer aan 100% veilig geld hebt en alle andere veilige mogelijkheden al hebt uitgeput. Er zijn inderdaad geen garanties in het beleggen maar dat sommige beleggingsvormen wel erg weinig risico hebben.

Schinnen-groen schreef op donderdag 17 juli 2014 @ 15:26:
[...]
Nogmaals: als je het geld prima kan missen, doen!! Maar heb je nog een hypo, of zo: aflossen.

Volgens mij is iedereen het hier daar wel over eens

[Bonsaiboom]

Dat zie je ook overal als devies - schulden afbouwen, kosten reduceren, en dan, als je over gaat houden, investeren (en dat kan op verschillende manieren). Zolang als je nog een hypotheek hebt, investeer je met geleend geld.

[Pooh]

Schinnen-groen schreef op donderdag 17 juli 2014 @ 14:52:
Elke belegging is een gok en als je dat, met de kennis van de afgelopen 10 jaar, nog niet hebt begrepen dan wordt het tijd om je toch eens achter de oren te krabben voordat je aan beleggen wilt beginnen.

Gokken moet je doen met geld dat je toch niet nodig hebt.

Dat is wel heel erg negatief. Een goede belegging is een investering, geen gok. Natuurlijk is er risico, maar op lange termijn is investeren in een goede portefeuille beter dan alleen maar rente krijgen op een spaarrekening.

En over die afgelopen 10 jaar, laten we een heel simpele vergelijking doen. Stel je hebt sinds 1991 elk jaar 10000 euro in de DAX (duitse aandelenindex, handig omdat die dividend meerekent) gestoken. Dan krijg je de bovenste van onderstaande grafieken.

En stel je was begonnen met dat te doen op de top van de markt, in 2000. Dan had je nog steeds een heel net rendement gehaald.

Let erop dat 'sparen' in onderstaande grafieken uitgaat van een rendement van 4%.

(En ja, bij investeren horen risico's. Als je je portefeuille ziet krimpen van 300k naar 150k tussen 2000 en 2003 is dat niet leuk. Als je zulke risico's niet kunt of wilt dragen moet je het niet doen.)

[ Voor 8% gewijzigd door Pooh op 17-07-2014 15:35 ]

[DeZaag]

Cloud schreef op donderdag 17 juli 2014 @ 15:30:
[...]

Volgens mij is iedereen het hier daar wel over eens

Dat betwijfel ik. Met de huidige lage hypotheekrente en het bestaan van HRA valt er best een case te maken dat beleggen rendabeler is dan het aflossen van de hypotheek.

Persoonlijk kies ik ervoor om beide te doen. Ik los het aflossingsvrije deel van m'n hypotheek maandelijks af en leg een vergelijkbaar bedrag eveneens maandelijks in voor de aanschaf van index trackers.

[MrAcid]

DeZaag schreef op donderdag 17 juli 2014 @ 15:35:
[...]


Dat betwijfel ik. Met de huidige lage hypotheekrente en het bestaan van HRA valt er best een case te maken dat beleggen rendabeler is dan het aflossen van de hypotheek.

Persoonlijk kies ik ervoor om beide te doen. Ik los het aflossingsvrije deel van m'n hypotheek maandelijks af en leg een vergelijkbaar bedrag eveneens maandelijks in voor de aanschaf van index trackers.

Inderdaad, zolang er HRA en hele lage hypotheekrentes zijn is het niet vanzelfsprekend de beste keuze om af te lossen. Ik heb zelf een hypotheek voor 3,79%, 10 jaar rentevast. Met HRA wordt dat netto nog een stukje minder (zeg zo'n 2,5%). Daar is wel tegenop te indexbeleggen.

Zelfde voor een studielening tegen <1%. Ik kan hem aflossen, maar het ik kies ervoor om dat met zo'n rente niet versneld te doen.

[Schinnen-groen]

Pooh schreef op donderdag 17 juli 2014 @ 15:33:
[...]

Dat is wel heel erg negatief. Een goede belegging is een investering, geen gok. Natuurlijk is er risico, maar op lange termijn is investeren in een goede portefeuille beter dan alleen maar rente krijgen op een spaarrekening.

En over die afgelopen 10 jaar, laten we een heel simpele vergelijking doen. Stel je hebt sinds 1991 elk jaar 10000 euro in de DAX (duitse aandelenindex, handig omdat die dividend meerekent) gestoken. Dan krijg je de bovenste van onderstaande grafieken.

En stel je was begonnen met dat te doen op de top van de markt, in 2000. Dan had je nog steeds een heel net rendement gehaald.

Let erop dat 'sparen' in onderstaande grafieken uitgaat van een rendement van 4%.

(En ja, bij investeren horen risico's. Als je je portefeuille ziet krimpen van 300k naar 150k tussen 2000 en 2003 is dat niet leuk. Als je zulke risico's niet kunt of wilt dragen moet je het niet doen.)

[afbeelding]

Mooie informatie met voor mensen die een beleggingshypo hebben. Die begrijpen dat allemaal.

sorry, kon het even niet laten.

[Pooh]

Schinnen-groen schreef op donderdag 17 juli 2014 @ 15:41:
[...]
Mooie informatie met mensen die een beleggingshypo hebben. Die begrijpen dat allemaal.

sorry, kon het even niet laten.

Beleggingshypotheken zijn op zich helemaal geen heel slechte producten. Ik heb een beleggingshypotheek gehad, en daarmee was ik een stuk gunstiger uit dan ik met welke andere vorm dan ook geweest zou zijn.

Maar er zijn veel beleggingshypotheken geweest die gewoon slechte producten waren:
- Hoge kosten
- Te hoog ingeschat rendement (tot 8% of zelfs meer)
- Belegginsverzekering (dus geen controle over waar het geld heenging, en extra kosten)
- Geen afnemend risico gedurende de looptijd (dus als de beurs in het laatste jaar 50% daalde had je ineens 50% minder)
- enzovoorts.

Maar dat heeft niks met beleggen 'an sich' te maken, alleen met de naiviteit van mensen die dachten dat ze snel rijk konden worden en banken die daar handig (of verwerpelijk, afhankelijk van hoe je kijkt) op inspeelden,

Beleggen zonder kennis, zonder overzicht, zonder plan door alleen maar een standaard-product van een bank af te nemen zou ik altijd afraden. Maar daarmee hoeft het nog niet meteen heel ingewikkeld of risicovol te zijn. Begin als je 20 bent met 100% aandelen en 0% obligaties, en schuif in 40 jaar tijd naar 100% obligaties en 0% aandelen, allemaal te beleggen in doodsaaie ETF's met lage TER en goede spreiding, en als je dat gewoon 40 jaar volhoudt weet ik zeker dat je beter af bent dan wanneer je je geld gewoon op een spaarrekening had gedumpt. Zeker omdat je portefeuille je ook zal beschermen tegen inflatie.

De huidige lage inflatie is leuk, maar er zijn genoeg mensen die zich nog kunnen herinneren hoe we hier 10% inflatie per jaar hadden. Dan is je spaargeld ook heel snel weg hoor, de spaarrentes uit die tijd hielden dat niet bij.

[Cloud]

MrAcid schreef op donderdag 17 juli 2014 @ 15:40:
[...]

Inderdaad, zolang er HRA en hele lage hypotheekrentes zijn is het niet vanzelfsprekend de beste keuze om af te lossen. Ik heb zelf een hypotheek voor 3,79%, 10 jaar rentevast. Met HRA wordt dat netto nog een stukje minder (zeg zo'n 2,5%). Daar is wel tegenop te indexbeleggen.

Het is in elk geval goed om er kritisch naar te kijken, dus uitrekenen. Het zal ongetwijfeld zijn dat aflossen niet altijd beter is op de korte termijn maar het is wel een veiliger optie dan beleggen. En lang niet iedereen heeft hypotheken met zulke lage rentes, ik in elk geval niet. Vergeet overigens een eventuele VRH niet hé

[MrAcid]

Zeker goed om er kritisch naar te kijken, ik zeg ook niet dat het altijd beter is. Vermogensbelasting moet je inderdaad ook rekening mee houden. Uitrekenen is daarom sowieso altijd slim, maar ik ga er eigenlijk vanuit dat iedereen in dit topic sowieso alle zaken voor zijn eigen (unieke) situatie narekent en bekijkt en niet zomaar alles overneemt wat hier wordt opgeschreven of beweerd.

Blijft een leuk en leerzaam topic dit!

Wat ik via Mr. Money Moustache tegenkwam: https://www.personalcapital.com/ - weet iemand of hier een goed Nederlands alternatief van is? Ik heb even snel een account aangemaakt maar het is echt voor 100% op de US gericht, dus het is voor ons amper bruikbaar - maar ziet er wel erg nuttig uit om goeie overzichten te maken. Ik "werk" nu vooral met Excel en dat voelt toch een beetje houtje-touwtje.

[Schinnen-groen]

Pooh schreef op donderdag 17 juli 2014 @ 15:49:
[...]

Beleggingshypotheken zijn op zich helemaal geen heel slechte producten. Ik heb een beleggingshypotheek gehad, en daarmee was ik een stuk gunstiger uit dan ik met welke andere vorm dan ook geweest zou zijn.

Maar er zijn veel beleggingshypotheken geweest die gewoon slechte producten waren:
- Hoge kosten
- Te hoog ingeschat rendement (tot 8% of zelfs meer)
- Belegginsverzekering (dus geen controle over waar het geld heenging, en extra kosten)
- Geen afnemend risico gedurende de looptijd (dus als de beurs in het laatste jaar 50% daalde had je ineens 50% minder)
- enzovoorts.

Maar dat heeft niks met beleggen 'an sich' te maken, alleen met de naiviteit van mensen die dachten dat ze snel rijk konden worden en banken die daar handig (of verwerpelijk, afhankelijk van hoe je kijkt) op inspeelden,

Beleggen zonder kennis, zonder overzicht, zonder plan door alleen maar een standaard-product van een bank af te nemen zou ik altijd afraden. Maar daarmee hoeft het nog niet meteen heel ingewikkeld of risicovol te zijn. Begin als je 20 bent met 100% aandelen en 0% obligaties, en schuif in 40 jaar tijd naar 100% obligaties en 0% aandelen, allemaal te beleggen in doodsaaie ETF's met lage TER en goede spreiding, en als je dat gewoon 40 jaar volhoudt weet ik zeker dat je beter af bent dan wanneer je je geld gewoon op een spaarrekening had gedumpt. Zeker omdat je portefeuille je ook zal beschermen tegen inflatie.

De huidige lage inflatie is leuk, maar er zijn genoeg mensen die zich nog kunnen herinneren hoe we hier 10% inflatie per jaar hadden. Dan is je spaargeld ook heel snel weg hoor, de spaarrentes uit die tijd hielden dat niet bij.

Ik proef uit je opmerking iets van: mensen die door een hypotheekverstrekker als advies kregen om een beleggingshypotheek af te sluiten zijn naïeve mensen.
Vind je dat een hypotheeknemer financiële kennis moet bezitten mbt de punten die je in je lijstje noemt?
Óf bedoel je dat ze zijn opgelicht door de boys uit die sector? Je gaat niet voor niets naar een hypotheekverstrekker of tussenpersoon (de Hypotheker, bijvoorbeeld). Dat doe je omdat je te weinig kennis van zaken op dat gebied hebt.

Wat je eigen hypo betreft: als je in een andere periode je beleggingshypo had gehad, was het allemaal misschien iets minder rooskleurig voor je geweest.

De bottom line is imho: resultaten uit het verleden geven geen......

[Bonsaiboom]

MrAcid schreef op donderdag 17 juli 2014 @ 15:40:
[...]

Inderdaad, zolang er HRA en hele lage hypotheekrentes zijn is het niet vanzelfsprekend de beste keuze om af te lossen. Ik heb zelf een hypotheek voor 3,79%, 10 jaar rentevast. Met HRA wordt dat netto nog een stukje minder (zeg zo'n 2,5%). Daar is wel tegenop te indexbeleggen.

Zelfde voor een studielening tegen <1%. Ik kan hem aflossen, maar het ik kies ervoor om dat met zo'n rente niet versneld te doen.

Dat kán, alleen besef je dat je wel belegd met geleend geld. En, als je genoeg overhoudt na je hypotheek betaling, en je voelt je comfortabel bij het feit dat dat wat je in je indexen stopt ook minder waard kan worden, dan neem je daar een bewuste beslissing voor. Je creeert dan een hefboom en die kunnen twee kanten op werken.

[Pooh]

Schinnen-groen schreef op donderdag 17 juli 2014 @ 16:13:
[...]


Ik proef uit je opmerking iets van: mensen die door een hypotheekverstrekker als advies kregen om een beleggingshypotheek af te sluiten zijn naïeve mensen.
Vind je dat een hypotheeknemer financiële kennis moet bezitten mbt de punten die je in je lijstje noemt?
Óf bedoel je dat ze zijn opgelicht door de boys uit die sector? Je gaat niet voor niets naar een hypotheekverstrekker of tussenpersoon (de Hypotheker, bijvoorbeeld). Dat doe je omdat je te weinig kennis van zaken op dat gebied hebt.

Wat je eigen hypo betreft: als je in een andere periode je beleggingshypo had gehad, was het allemaal misschien iets minder rooskleurig voor je geweest.

De bottom line is imho: resultaten uit het verleden geven geen......

Over adviseurs: Lastige vraag. Ik heb zelf altijd net zo lang doorgevraagd totdat ik het begreep. Waaraan verdient de tussenpersoon zijn geld, hoeveel geld krijgt hij, waaraan moet ik mijn geld verdienen, waarom is dat realistisch? Dingen die ik niet begrijp wil ik niet hebben.

Maar ik ben daarin vrij extreem, en ik hou graag de touwtjes in handen. Het is te kort door de bocht om de rest van de mensen maar 'naief' te noemen. Wat dat betreft had er meer controle op advies moeten zijn. En misschien moet je inderdaad gewoon een examen afleggen voordat je zo'n product mag kopen.

Wat betreft mijn hypotheek: Die had ik in een slechte periode, maar ik had een mooi product. Verpande beleggingsrekening, vrijheid om zelfstandig te beleggen, lage kosten.

[Schinnen-groen]

Pooh schreef op donderdag 17 juli 2014 @ 16:18:
[...]

Over adviseurs: Lastige vraag. Ik heb zelf altijd net zo lang doorgevraagd totdat ik het begreep. Waaraan verdient de tussenpersoon zijn geld, hoeveel geld krijgt hij, waaraan moet ik mijn geld verdienen, waarom is dat realistisch? Dingen die ik niet begrijp wil ik niet hebben.

Maar ik ben daarin vrij extreem, en ik hou graag de touwtjes in handen. Het is te kort door de bocht om de rest van de mensen maar 'naief' te noemen. Wat dat betreft had er meer controle op advies moeten zijn. En misschien moet je inderdaad gewoon een examen afleggen voordat je zo'n product mag kopen.

Wat betreft mijn hypotheek: Die had ik in een slechte periode, maar ik had een mooi product. Verpande beleggingspolis, vrijheid om zelfstandig te beleggen, lage kosten.

Je hebt dus geen "doorsnee beleggingshypo" gehad, begrijp ik. Voor de andere 98% van de beleggingshypotheeknemers (3x woordwaarde) zal dat waarschijnlijk wel het geval zijn geweest.

En misschien moet je inderdaad gewoon een examen afleggen voordat je zo'n product mag kopen.

Ik denk trouwens niet dat dit voorstel Europees wordt aangenomen. Daar zullen ook de meesten niet voor slagen. Daarom zijn er hypotheekadviseurs verzonnen

[Pooh]

Examen voor hypotheek is niet nodig. Gewoon standaard lineair of annuitair, vaste rente, klaar.

Maar voor beleggen (zeker als dat voor aflossing hypotheek is) zou ik een examen geen slecht idee vinden.

[Bonsaiboom]

Ik vind die financiele bijsluiters anders ook al erg duidelijk. Cijfers 1 t/m 7 wbt risico. Hier zou nog iets bijkunnen als "Je kan hierbij heel je inleg verliezen" of "Je kan hierbij MEER dan heel je inleg verliezen".

[Pooh]

Bonsaiboom schreef op donderdag 17 juli 2014 @ 16:36:
Ik vind die financiele bijsluiters anders ook al erg duidelijk. Cijfers 1 t/m 7 wbt risico. Hier zou nog iets bijkunnen als "Je kan hierbij heel je inleg verliezen" of "Je kan hierbij MEER dan heel je inleg verliezen".

Ik mis in die dingen de helft van het verhaal:
- Je adviseur krijgt voor het afsluiten van dit product bedrag X
- Je adviseur krijgt tijdens de looptijd van dit product elke maand bedrag Y
- Je betaalt aan rechtstreekse kosten Z
- Je betaalt aan indirecte kosten (bijvoorbeeld door een fonds van fondsen te kopen) nog eens ZZ
- Als je dit vergelijkt met de 'standaardoplossingen' (eenvoudige ETF, spaarrekening, etc), zijn de extra kosten ZZZ%
- etc...

[JvdS]

MrAcid schreef op donderdag 17 juli 2014 @ 15:56:
Wat ik via Mr. Money Moustache tegenkwam: https://www.personalcapital.com/ - weet iemand of hier een goed Nederlands alternatief van is? Ik heb even snel een account aangemaakt maar het is echt voor 100% op de US gericht, dus het is voor ons amper bruikbaar - maar ziet er wel erg nuttig uit om goeie overzichten te maken. Ik "werk" nu vooral met Excel en dat voelt toch een beetje houtje-touwtje.

Naar zo'n soort website ben ik ook al een tijd op zoek. Zonde dat er zoiets niet voor Nederland is!

[hv08]

Wat let ons om het zelf te maken

[JvdS]

Daar zat ik ook aan te denken .

[Z___Z]

Bonsaiboom schreef op donderdag 17 juli 2014 @ 15:32:
Dat zie je ook overal als devies - schulden afbouwen, kosten reduceren, en dan, als je over gaat houden, investeren (en dat kan op verschillende manieren). Zolang als je nog een hypotheek hebt, investeer je met geleend geld.

Als je denkt dat als je een hypotheek hebt en tegelijkertijd belegt, je met geleend geld belegt, dan moet je inderdaad niet gaan beleggen en je financiele kennis verhogen.

[Don Quijote]

Voel ik hier een project aankomen .
Ik gebruik nu AFAS, maar begin tegen wat limitaties aan te lopen. Zoals het bijhouden van je aandelen portefeuille. Ben het nu allemaal handmatig in "kas boeken" aan het bij houden. Maar dat kan beter.

[JvdS]

DivWhis schreef op donderdag 17 juli 2014 @ 17:33:
Voel ik hier een project aankomen .
Ik gebruik nu AFAS, maar begin tegen wat limitaties aan te lopen. Zoals het bijhouden van je aandelen portefeuille. Ben het nu allemaal handmatig in "kas boeken" aan het bij houden. Maar dat kan beter.

Ik maakte voorheen ook gebruik van AFAS, maar begon me op een gegeven moment te irriteren aan zaken die niet goed werkten. Bovendien mist het functionaliteit zoals het goed bij kunnen houden van beleggingen.
Een all-in-one app zoals hierboven zou mooi zijn. Moet in de toekomst ook mogelijk zijn omdat lijkt alsof de banken hun mutaties via een API beschikbaar moeten maken.

[icecreamfarmer]

DivWhis schreef op donderdag 17 juli 2014 @ 17:33:
Voel ik hier een project aankomen .
Ik gebruik nu AFAS, maar begin tegen wat limitaties aan te lopen. Zoals het bijhouden van je aandelen portefeuille. Ben het nu allemaal handmatig in "kas boeken" aan het bij houden. Maar dat kan beter.

Ik gebruik google docs.
Tot nu toe werkt dat erg goed, beurskoersen worden elke 20min geupdate.
Verder sparrekeningen houd ik zelf bij maar het is vooral de lopende rekening die fluctueert.

[Bonsaiboom]

Z___Z schreef op donderdag 17 juli 2014 @ 17:32:
[...]

Als je denkt dat als je een hypotheek hebt en tegelijkertijd belegt, je met geleend geld belegt, dan moet je inderdaad niet gaan beleggen en je financiele kennis verhogen.

Leg het mij dan eens anders uit? Ik snap heus wel dat je onderpand tegenover je hypotheek hebt staan en dat je daarmee een netto positieve vermogenspositie kan hebben als je een hypotheek hebt. Dan nog, je zit gewoon in een hefboom situatie, en je vermindert die hefboom niet door te beleggen ipv af te lossen. Stel dat de situatie andersom is, en je bent hypotheekvrij alleen hebt geen spaargeld meer. Je neemt nu een hypotheek van 10k om dit op de beurs te investeren. Is het dan wel geleend geld?

[Shapeshifter]

DivWhis schreef op donderdag 17 juli 2014 @ 17:33:
Voel ik hier een project aankomen .
Ik gebruik nu AFAS, maar begin tegen wat limitaties aan te lopen. Zoals het bijhouden van je aandelen portefeuille. Ben het nu allemaal handmatig in "kas boeken" aan het bij houden. Maar dat kan beter.

Ik heb gewoon zelf een webapp gemaakt waar ik mijn rekeningen in kan importeren en categorieën kan toekennen. Ik kan over willekeurige perioden inkomsten en uitgaven tegen elkaar zetten (helemaal terug tot aan dat mijn eerste rekening geopend werd ) en deze worden ook automatisch vergeleken met wat er begroot is, zo kan ik snel zien of het ergens misgaat. Tevens kan ik per categorie in de tijd kijken of ik ergens steeds meer aan ben gaan uitgeven. Was wel wat werk, maar als ik nu denk: "ik zou eigenlijk dat willen vergelijken" kost het eigenlijk weinig moeite om het erbij te maken en mijn data blijft lekker in mijn eigen huis (draait op mijn NAS), ook een prettige gedachte.

[Cloud]

Het is inderdaad niet beleggen met geleend geld in de meest letterlijke zin maar je zou prima kunnen beargumenteren dat geld dat je had kúnnen gebruiken om je hypotheekschuld mee af te lossen, gebruiken voor beleggingen, een vorm van beleggen met geleend geld is. Want het is wel degelijk geleend geld, al heb je het dan niet geleend voor dat specifieke doel en ook al is er onderpand.

Denk eens verder en kijk naar dezelfde situatie met een hypotheek die onder water staat. Als je dan geld 'over' hebt en je gaat dat gebruiken om te beleggen. Is het dan wel geleend geld (nog even afgezien van het feit dat het oliedom is)?

edit:

Dat Personal Capital ziet er inderdaad erg fijn uit. Bijzonder jammer dat zoiets nog niet bestaat voor de NL markt. Ik denk niet dat het vlot in elkaar te draaien is, gezien de koppelingen die ze lijken te hebben met andere financiële dienstverleners.

[ Voor 17% gewijzigd door Cloud op 17-07-2014 20:01 ]

[Verwijderd]

MrAcid schreef op donderdag 17 juli 2014 @ 12:26:
Ik heb een sheetje in elkaar geknutseld waarmee je het kunt berekenen. Feel free to use:
https://dl.dropboxusercon...illende%20aanbieders.xlsx

Heb niet al teveel verklaringen opgenomen dus het is mogelijk even puzzelen voor je doorhebt hoe hij ingevuld moet worden. De "roze kleurige" cellen moet je zelf invullen.

Periodieke inleg = maandelijks
Servicefee = jaarlijkse fee (bewaarloon - dus niet de TER)

De vermogensopbouw wordt niet helemaal netjes berekend (per jaar, niet per maand) waardoor de kosten niet 100% kloppen, maar het geeft een goed genoeg beeld voor mijn eigen gebruik.

Mooi gedaan!

Maar, deze sheet gaat voorbij aan het feit dat veel gebruikers van Binck Basic niet elke maand inleggen: dat is onvoordelig door de hoge vast transactiekosten. Veel gebruikers van Binck wachten tot ze 2000 bij elkaar hebben, zodat de transactiekosten ongeveer 0.5% zijn. Als je dus elke maand 500 euro wilt sparen, zou je bij Binck elke 4 maanden kunnen inleggen. Spaar je 200 euro per maand, dan zou je elke 10 maanden kunnen inleggen.

[ Voor 3% gewijzigd door Verwijderd op 17-07-2014 21:46 ]

[MisterBlue]

Cloud schreef op donderdag 17 juli 2014 @ 19:59:
Het is inderdaad niet beleggen met geleend geld in de meest letterlijke zin maar je zou prima kunnen beargumenteren dat geld dat je had kúnnen gebruiken om je hypotheekschuld mee af te lossen, gebruiken voor beleggingen, een vorm van beleggen met geleend geld is. Want het is wel degelijk geleend geld, al heb je het dan niet geleend voor dat specifieke doel en ook al is er onderpand.

Als ik wil investeren in mijn eigen onderneming ga ik niet eerst wachten tot ik mijn hypotheek heb afgelost. Zo zie ik beleggen op de beurs ook: investeren in ondernemingen van anderen. Als je het hebt over speculeren op de beurs geef ik je wel gelijk.

[Config]

We glijden weer lekker af naar het beoordelen van elkaars gedrag

Beleggen met geleend geld voor ~1,5% (=netto hypotheekrente) is geen schande IMO. Het afbetalen zou op zijn minst financieel onhandig zijn: de som klopt gewoon niet als je beleggen als optie ziet.

[Pooh]

Config schreef op donderdag 17 juli 2014 @ 21:50:
We glijden weer lekker af naar het beoordelen van elkaars gedrag

Beleggen met geleend geld voor ~1,5% (=netto hypotheekrente) is geen schande IMO. Het afbetalen zou op zijn minst financieel onhandig zijn: de som klopt gewoon niet als je beleggen als optie ziet.

Het heeft weinig met de rente te maken, veel meer met het risico. Als je belegt met een groot bedrag aan geleend geld, en je belegging zou ineens waardeloos zijn, dan zit je met een schuld die je nooit kunt afbetalen.
Als je belegt om je hypotheek af te betalen, en je belegging zou ineens waardeloos zijn, dan is het ergste wat je kan gebeuren dat je je huis moet verkopen en ergens wat moet huren.

Dat maakt nogal wat uit.

[Fimke]

Hoe berekenen jullie je spaarratio? Wij hebben beide inkomen uit werk en ontvangen maandelijks kinderopvangtoeslag. Nu tel ik dat bij inkomen op. Of doe je dat niet en doe je als uitgave de netto kinderopvangkosten? Zelfde geldt voor hypotheekrente. Het maakt voor de uitkomst nogal uit.

[Sibylle]

De uitkomst is niet belangrijk, wat belangrijk is is de kosten die je later hebt. Tenminste, ik ga uit van 'uitkomst' als in hoelang je moet sparen voor FO.

Later als je FO bent dan heb je geen kinderopvangkosten of toeslag en hypotheekrenteaftrek. Dus in je berekening moet je rekenen met de kosten die je later als FO gaat maken per maand, en het bedrag dat je NU spaart pak je als percentage daarvan.
Zoals je ziet zijn deze berekeningen erg scheef en klopt er weinig van.

Of gaat het je puur om een index voor jezelf (als 'uitkomst')? Dan moet je het zelf weten, als je het maar consistent doet en goed corrigeert als je kindersituatie verandert.

Ik kijk gewoon naar totaal netto ontvangen in een jaar, en totaal niet uitgegeven in een jaar.

[Config]

Pooh schreef op donderdag 17 juli 2014 @ 22:44:
[...]
Als [...] je belegging zou ineens waardeloos (zou) zijn

Hoe groot schat jij de kans dat West-Europese landen failliet gaan?

[ Voor 10% gewijzigd door Config op 17-07-2014 23:13 ]

[Pooh]

Config schreef op donderdag 17 juli 2014 @ 23:11:
[...]

Hoe groot schat jij de kans dat West-Europese landen failliet gaan?

Landen gaan niet failliet, maar daar kun je dan ook niet in beleggen. De kans dat een staatsobligatie niet wordt terugbetaald is klein maar reeel.

Maar goed, zelfs als je 20% verliest op een belegging (in het geval van obligaties is dat heel eenvoudig als de rente een keer flink omhooggaat), kom je bij geleend geld al goed in de problemen. Mijn betoog inkorten tot alleen het extreme voorbeeld heeft natuurlijk geen enkel nut.

[kmf]

Dit is ook een manier van FO zijn. Maar wel een beetje te extreem naar mijn zin. http://www.dailymail.co.u...r-theres-no-bathroom.html

[rr7r]

Spaartax in Spanje van 0,03%. Het CDA heeft ook aan de ontwerptafel gezeten, want het wordt met terugwerkende kracht ingevoerd (1-1-2014). Binnenkort ook in andere EU-landen te verwachten?

NL versie.

[merauder]

Fimke schreef op donderdag 17 juli 2014 @ 22:45:
Hoe berekenen jullie je spaarratio? Wij hebben beide inkomen uit werk en ontvangen maandelijks kinderopvangtoeslag. Nu tel ik dat bij inkomen op. Of doe je dat niet en doe je als uitgave de netto kinderopvangkosten? Zelfde geldt voor hypotheekrente. Het maakt voor de uitkomst nogal uit.

Qua spaarratio hanteer ik zelf ( netto-inkomen ) minus de (indien van toepassing bruto) lasten. Al het andere, zoals bijvoorbeeld belastingteruggaaf, inkomen uit overige werkzaamheden of toeslagen zie ik zelf als extra's, en die worden doorgesluisd naar de spaarrekening.

Op dit moment kan ik +/- 40% van mijn inkomen sparen, in de praktijk is dit slechts 25% (soms leef ik iets te ruim)

Juist omdat spaargeld dood geld is, wil ik hier niet meer teveel van hebben, en splits ik alles op in diverse potjes. Ik hanteer op dit moment de volgende posten:

1. Potje van € 5000,- voor reparaties / vervangingen inventaris.
2. Potje van € 5000,- voor onvoorziene vervoerskosten.

Voor al het overige stel ik spaardoelen, zoals bijvoorbeeld de tuin op laten knappen, een vakantie, een andere auto of grote klussen aan mijn woning.

[Henk007]

rr7r schreef op vrijdag 18 juli 2014 @ 02:21:
Spaartax in Spanje van 0,03%. Het CDA heeft ook aan de ontwerptafel gezeten, want het wordt met terugwerkende kracht ingevoerd (1-1-2014). Binnenkort ook in andere EU-landen te verwachten?

NL versie.

Geen enkel probleem mee, tenminste als de 1,2% VRH wordt afgeschaft

[Schinnen-groen]

rr7r schreef op vrijdag 18 juli 2014 @ 02:21:
Spaartax in Spanje van 0,03%. Het CDA heeft ook aan de ontwerptafel gezeten, want het wordt met terugwerkende kracht ingevoerd (1-1-2014). Binnenkort ook in andere EU-landen te verwachten?

NL versie.

In principe is dit een aanpassing aan de VRH.
De zaak wordt dan gestaffeld:

- tot aan het "belastingvrije bedrag": 0,03%
- vanaf dat niveau: 1,23%

[Bonsaiboom]

Het geldt alleen voor spaargeld? Niet voor investeringen, en andere box3 zaken. Het is dus wel een additionele belasting.

[Hbeez]

Pooh schreef op donderdag 17 juli 2014 @ 23:28:
[...]

Mijn betoog inkorten tot alleen het extreme voorbeeld heeft natuurlijk geen enkel nut.

Je geeft zelf als voorbeeld dat je dakloos op straat kan komen te staan door te beleggen met geleend geld, dat is ook een extreem voorbeeld.

Ik vind dat 'beleggen met geleend geld' hier wordt verward met beleggingen waar ook schulden tegenover staan. Naar de bank gaan om een ton te lenen om te speculeren op de beurs is natuurlijk een hele andere situatie dan bv. een gedeelte van je spaargeld beleggen terwijl je ook nog een oude studieschuld hebt of een hypotheek. Ik heb zelf ook een studieschuld maar ook spaargeld; dan is het een kwestie van rentes vergelijken en risico's overwegen om te bepalen of ik beter kan gaan beleggen of de studieschuld aflossen. Vanwege de 1.5% rente op de studieschuld is de keuze snel gemaakt.

[Config]

Ik had het zelf al opgegeven, maar wat jij zegt Hbeez

[Verwijderd]

Schinnen-groen schreef op vrijdag 18 juli 2014 @ 08:24:
[...]

In principe is dit een aanpassing aan de VRH.
De zaak wordt dan gestaffeld:

- tot aan het "belastingvrije bedrag": 0,03%
- vanaf dat niveau: 1,23%

Dat zou ik een opmerkelijk besluit vinden gezien de tijdsgeest. Je hoort de laatste tijd meer a la Piketty dat lage vermogens minder belast zullen worden en de hogere meer.
Daarnaast, subtiel maar belangrijk verschil, hebben wij het in NL niet over een spaartax, maar over een vermogensrendementheffing.

[Schinnen-groen]

Ik had bijna gezegd: "Dat zal in Nederland wel niet gebeuren".
Maar ik ben de laatste jaren ERG voorzichtig geworden met dit soort uitspraken....

[icecreamfarmer]

Verwijderd schreef op vrijdag 18 juli 2014 @ 09:02:
[...]


Dat zou ik een opmerkelijk besluit vinden gezien de tijdsgeest. Je hoort de laatste tijd meer a la Piketty dat lage vermogens minder belast zullen worden en de hogere meer.
Daarnaast, subtiel maar belangrijk verschil, hebben wij het in NL niet over een spaartax, maar over een vermogensrendementheffing.

Klopt maar die komt wel op hetzelfde neer omdat er niet naar je rendement gekeken wordt.

[Config]

Verwijderd schreef op vrijdag 18 juli 2014 @ 09:02:
Daarnaast, subtiel maar belangrijk verschil

Waarom belangrijk?