[C#][discussie] Lekker veel var gebruiken?

[RayNbow]

Snake schreef op donderdag 11 februari 2010 @ 14:01:
[...]

Waarom zou je dat uberhaupt doen? Zet dan ipv dat ? IEnumerable<int> ofzo

+ als dat zou compileren, hoe zou de compiler dan moeten kunnen afleiden of select er uberhaupt op werkt?

Dan werkt addOne alleen op IEnumerable<int>s. Ik wil dat addOne voor elke C<int> werkt, waarbij C de Select() LINQ operator ondersteunt. C#'s type system is niet krachtig genoeg om de LINQ operators in een of meerdere interfaces op te vangen (wegens gebrek aan higher-kinded polymorphism).

Verwijderd schreef op donderdag 11 februari 2010 @ 14:09:
[...]

Ik denk dat ik de strekking van het voorafgaande betoog mis maar het volgende compileert prima, zonder warnings, in Java.

Java:

List<String> strings = newArrayList();//compileert zonder warnings
    
    public static<E> List<E> newArrayList() {
        return new ArrayList<E>();
    }

Ik beweer nergens dat dat warnings oplevert?

.oisyn schreef op donderdag 11 februari 2010 @ 14:32:
Ik zei toch al dat het evidoth's opmerking was die mij op het verkeerde been zette?

Daar kwam ik ook achter tijdens het typen van m'n vorige reactie. Vandaar dat stuk tussen haakjes in de eerste alinea.


* RayNbow slaat .oisyn. Niet stiekem dingen erbij tikken!

.oisyn schreef op donderdag 11 februari 2010 @ 14:32:
Vind je het gek dat dat niet kan, ik snap niet eens wat je nou eigenlijk probeert te doen, hoe moet een compiler dat dan snappen

Op het vraagteken kun je zoals hierboven opgemerkt IEnumerable invullen. Maar je zou ook een andere interface/class-naam invullen, zolang het maar Select(Func<A,B>) ondersteunt. C# dwingt me nu eig. om dit te typen:

C#:

static IEnumerable<int> addOne(IEnumerable<int> xs) 
{ 
    return from x in xs 
           select x + 1; 
}
static IObservable<int> addOne(IObservable<int> xs)   // (IObservable uit Rx)
{ 
    return from x in xs 
           select x + 1; 
}

static Foo<int> addOne(Foo<int> xs) 
{ 
    return from x in xs 
           select x + 1; 
}
static Bar<int> addOne(Bar<int> xs) 
{ 
    return from x in xs 
           select x + 1; 
}
// enzovoorts... voor elke class/interface die de LINQ Select operator bevat...

[ Voor 27% gewijzigd door RayNbow op 11-02-2010 14:48 ]

[Snake]

Er moet toch ergens een relatie tussen die types zijn? En die zijn er momenteel niet. Dus dan kan je toch niets omgekeerd 'generic' maken?

[Woy]

RayNbow schreef op donderdag 11 februari 2010 @ 14:38:
[...]
Op het vraagteken kun je zoals hierboven opgemerkt IEnumerable invullen. Maar je zou ook een andere interface/class-naam invullen, zolang het maar Select(Func<A,B>) ondersteunt. C# dwingt me nu eig. om dit te typen:

Dat komt meer doordat Select een extension method is, en er is geen manier om een constraint te leggen op welke extension methods er minstens moeten zijn. Als Select in een interface of base-type had gezeten dan was het geen probleem geweest.

[RayNbow]

Woy schreef op donderdag 11 februari 2010 @ 15:23:
[...]

Dat komt meer doordat Select een extension method is, en er is geen manier om een constraint te leggen op welke extension methods er minstens moeten zijn. Als Select in een interface of base-type had gezeten dan was het geen probleem geweest.

Het gebrek aan higher-kinded polymorphism zorgt ervoor dat je de LINQ query operators niet in een interface kan stoppen.

Higher-kinded C# zou er ongeveer zo uit kunnen zien:

C#:

// Higher-kinded C#
interface IFunctor<F>
{
    F<B> Select(this F<A>, Func<A,B>);
}

interface IMonad<M> : IFunctor<M>
{
    M<B> SelectMany(this M<A>, Func<A, M<B>>);
}

static F<int> addOne<F>(F<int> xs) where F : IFunctor<F>
{  
    return from x in xs  
           select x + 1;  
} 

[Grijze Vos]

Tja, C# is nou eenmaal geen functionele taal. Misschien moet je gewoon F# gaan gebruiken?

Overigens, normaal gesproken hoor je gewoon IEnumerable te implementeren als je Linq ondersteunt, dus dan zou dat geen issue moeten zijn.

[ Voor 44% gewijzigd door Grijze Vos op 11-02-2010 18:20 ]

[RayNbow]

Grijze Vos schreef op donderdag 11 februari 2010 @ 18:19:
Tja, C# is nou eenmaal geen functionele taal. Misschien moet je gewoon F# gaan gebruiken?

Het doel van higher-kinded polymorphism is hetzelfde van polymorfisme: abstractie. Het ook kunnen abstraheren over typeconstructors ipv alleen types is niet iets dat alleen voor functionele talen is weggelegd.

Overigens, normaal gesproken hoor je gewoon IEnumerable te implementeren als je Linq ondersteunt, dus dan zou dat geen issue moeten zijn.

Dit is juist een grote misvatting. Het ondersteunen van LINQ staat niet gelijk aan het implementeren van IEnumerable. IEnumerable types zijn, zoals de naam van de interface al zegt, enumereerbaar. Je hoeft niet enumereerbaar te zijn om LINQ te kunnen implementeren. Een voorbeeld is een functie. Kan je elke functie enumereren?

De Select operator voor functies:

C#:

public static Func<E, B> Select<E, A, B>(this Func<E, A> f, Func<A, B> g)
{
    return x => g(f(x));
}

Voorbeeldje:

C#:

var res = (from x in (Func<int,int>)(x => x+1)
           select -x)(3);
Console.WriteLine(res); // schrijft netjes -4 naar het scherm

En wat dacht je van IObservable? IObservable is de duale van IEnumerable (zit in Reactive Extensions for .NET (Rx)) en implementeert ook de LINQ operators.

Edit: wat Rx sample code, gebaseerd op deze ietwat outdated video tutorial.

C#:

// drag/drop van een image in een canvas:
var mouseDown = from evt in Observable.FromEvent<MouseButtonEventArgs>(this, "MouseDown")
                select evt.EventArgs.GetPosition(this);

var mouseUp = from evt in Observable.FromEvent<MouseButtonEventArgs>(this, "MouseUp")
              select evt.EventArgs.GetPosition(this);

var mouseMove = from evt in Observable.FromEvent<MouseEventArgs>(this, "MouseMove")
                select evt.EventArgs.GetPosition(this);

var q = from start in mouseDown
        from delta in mouseMove.StartWith(start).TakeUntil(mouseUp)
                        .Let(mm => mm.Zip(mm.Skip(1), (prev, cur) =>
                            new { X = cur.X - prev.X, Y = cur.Y - prev.Y }))
        select delta;

q.ObserveOn(SynchronizationContext.Current).Subscribe(value =>
{
    Canvas.SetLeft(image, Canvas.GetLeft(image) + value.X);
    Canvas.SetTop(image, Canvas.GetTop(image) + value.Y);
});

[ Voor 27% gewijzigd door RayNbow op 11-02-2010 22:43 ]

[pedorus]

Je legt nu prima uit dat select eigenlijk gewoon de functie 'Select' aanroept. Het probleem is dan ook met jouw voorstel je niet eens een ?<int> hoeft te hebben om een select op die ints te doen. Dus iets als:

C#:

    class TestSelect
    {
        public IEnumerable<TResult> Select<TResult>(Func<int, TResult> selector)
        {
            for (int i = 0; i < 100; i++)
                yield return selector(100); 
        } 
    }

Hoe zou jouw AddOne hier moeten gaan werken? Dan zou je al moeten binden aan classes die een functie Select hebben die een Func<int, TResult> accepteert. Lijkt me niet een common use case met veel praktisch nut, en ook niet iets dat makkelijk te fixen is.

.oisyn schreef op donderdag 11 februari 2010 @ 13:19:
[...]

Een dictionary is geen map. Een map is namelijk georderd, een dictionary niet. Een map kan dus range queries afhandelen, en daaruit blijkt meteen ook waarom een map<K,list<V>> onhandig is - je kunt niet makkelijk over een range van elementen itereren, wat met een multimap wel kan.

Ik denk dat het iets uit de c-wereld is om zo te denken. In java, of hier in Google's implementatie, is een ArrayListMultimap intern zeer vergelijkbaar met een Dictionary<TKey,List<TValue>>. En als er iets anders werd bedoelt heb ik gelukkig var gebruikt, dat spaart weer werk bij veranderen.

---

Terug over var. Ik vond dit eigenlijk wel een mooi voorbeeld:

Kayshin schreef op woensdag 27 januari 2010 @ 13:17:

C#:

Uri baseNetTcpAddress = new Uri("net.tcp://localhost:9000");
ServiceHost host = new ServiceHost(typeof(PingService), new Uri[] { baseNetTcpAddress });
ServiceMetadataBehavior metadataBehavior = new ServiceMetadataBehavior();
host.Description.Behaviors.Add(metadataBehavior);
System.ServiceModel.Channels.Binding mexTcpBinding =
System.ServiceModel.Description.MetadataExchangeBindings.CreateMexTcpBinding();

host.AddServiceEndpoint(typeof(IMetadataExchange), mexTcpBinding, "mex");
host.AddServiceEndpoint(typeof(IOrderPizza), new NetTcpBinding(SecurityMode.None, true), string.Empty);
host.Open();

Zonder de volgorde te veranderen, en door enkel te snijden in typeaanduidingen, wordt het wat mij betreft al een stuk duidelijker:

C#:

            var baseNetTcpAddress = new Uri("net.tcp://localhost:9000");
            var host = new ServiceHost(typeof(PingService), baseNetTcpAddress);
            var metadataBehavior = new ServiceMetadataBehavior();
            host.Description.Behaviors.Add(metadataBehavior);
            var mexTcpBinding = MetadataExchangeBindings.CreateMexTcpBinding();

            host.AddServiceEndpoint(typeof(IMetadataExchange), mexTcpBinding, "mex");
            host.AddServiceEndpoint(typeof(IOrderPizza),
                new NetTcpBinding(SecurityMode.None, true), "");
            host.Open();

[.oisyn]

pedorus schreef op donderdag 11 februari 2010 @ 22:55:
Ik denk dat het iets uit de c-wereld is om zo te denken. In java, of hier in Google's implementatie, is een ArrayListMultimap intern zeer vergelijkbaar met een Dictionary<TKey,List<TValue>>. En als er iets anders werd bedoelt heb ik gelukkig var gebruikt, dat spaart weer werk bij veranderen.

Nee, dat heeft geen zak met C te maken . Geordende containers zijn essentieel voor bepaalde algoritmen. Als ik een map<int, string> heb, dan kan ik in O(log n + k) alle strings enumereren binnen een bepaald range van integers. Dat kan met een dictionary/hashmap niet, omdat die ongeordend zijn. Dat is dus het ene verschil.

Het andere verschil is het multi gedeelte; je zou een multimap<int, string> kunnen definieren als een map<int, list<string>>. Het enumereren over elementen wordt dan ingewikkelder, omdat ik niet alleen over de elementen van de multimap heen moet lopen, maar ook nog eens over de elementen van de list. Daar is dan een geneste loop voor nodig, tenzij je een iterator/enumerator schrijft die die poespas voor je afhandelt. Maar het is hoe dan ook meer werk en meer complexiteit. Een multimap is in dat opzicht gewoon praktischer.

Het verschil met de dictionary is dat het dan niet zo boeit, omdat je toch niet zo snel over meerdere elementen in de dictionary zou lopen, maar louter over de meerdere elementen met dezelfde key. Voor die usecase is een dictionary<int, list<string>> prima geschikt, en geen reden om een multimap<int, string> te gebruiken.

[ Voor 3% gewijzigd door .oisyn op 12-02-2010 00:14 ]

[RayNbow]

pedorus schreef op donderdag 11 februari 2010 @ 22:55:
Je legt nu prima uit dat select eigenlijk gewoon de functie 'Select' aanroept.

In dit simpele geval, ja. In iets uitgebreidere queries zoals met meerdere from-clauses wordt de query syntax vertaald naar SelectMany-aanroepen.

Het probleem is dan ook met jouw voorstel je niet eens een ?<int> hoeft te hebben om een select op die ints te doen.

Wat is dat voor redenatie? Als ik nu een IEnumerable<int> heb, maar ook een IObservable<int>, dan moet ik dus maar mijn addOne functie twee keer schrijven? Of stel je voor dat ik op een of andere manier die IObservable met een hamer bewerk totdat het in de vorm van IEnumerable past?

Dus iets als:

C#:

    class TestSelect
    {
        public IEnumerable<TResult> Select<TResult>(Func<int, TResult> selector)
        {
            for (int i = 0; i < 100; i++)
                yield return selector(100); 
        } 
    }

Hoe zou jouw AddOne hier moeten gaan werken? Dan zou je al moeten binden aan classes die een functie Select hebben die een Func<int, TResult> accepteert.

Ik volg je niet. Het gaat er niet om dat ik een Func<int,B> wil toepassen op ints, zoals je hierboven doet. Het gaat erom dat ik een functie wil kunnen toepassen op alle mogelijke functors, niet alleen op een select gezelschap onder de noemer IEnumerable<int>.

Lijkt me niet een common use case met veel praktisch nut,

Mijn addOne is niets anders dan een simpel, kunstmatig voorbeeld om aan te tonen dat zonder higher-kinded polymorphism ik meerdere keren een functie moet schrijven, waarbij de body exact hetzelfde is en alleen de type signature verschilt.

Momenteel is het praktische nut nog niet heel erg groot, maar dat komt omdat er nog weinig andere classes zijn die de LINQ operators implementeert. Standaard heb je alleen alle IEnumerable en IQueryable classes en sinds kort kun je spelen met Rx's IObservable classes. Nu kun je er nog mee wegkomen om 1 extra kopie te maken met alleen een andere type signature...

...maar wanneer je zo'n extra kopie maakt, heb je je dan in feite jezelf niet herhaald? Is dat misschien niet net zo erg als de herhaling in "List<string> stringList = new List<string>();"?

en ook niet iets dat makkelijk te fixen is.

Het is ook lastig te fixen, maar dat verandert weinig aan m'n mening dat C#'s type system niet erg krachtig is.

.oisyn schreef op vrijdag 12 februari 2010 @ 00:12:
Nee, dat heeft geen zak met C te maken . Geordende containers zijn essentieel voor bepaalde algoritmen. Als ik een map<int, string> heb, dan kan ik in O(log n + k) alle strings enumereren binnen een bepaald range van integers. Dat kan met een dictionary/hashmap niet, omdat die ongeordend zijn. Dat is dus het ene verschil.

Misschien wel met het jargon dat C of C++ proggers gebruiken, waarin map dus blijkbaar refereert naar een datastructuur met de eigenschap dat de keys geordend zijn. Voor mij is een map conceptueel niets anders dan een afbeelding van keys naar values.

[Neverwinterx]

Ik vind het wat vreemd dat dit wordt aangehaald als een goed gebruik van var:

Java:

List<String> bad = new ArrayList<String>();
var good = new ArrayList<String>();

Een goed systeem (zoals in Java 7 zal komen) zou dit moeten kunnen doen:

Java:

List<String> best = new ArrayList<>();

Een wat uitgebreider voorbeeld:

Java:

Map<String, List<String>> anagrams = new HashMap<>();

Dat vermijdt ook de verbositeit, maar sleurt er niet iets obscuur als var bij.
(http://mail.openjdk.java....2009-February/000009.html)

[RayNbow]

Dat vermijdt de verbositeit in Java alleen bij het instantiëren.

[ Voor 13% gewijzigd door RayNbow op 12-02-2010 00:36 ]

[Wolfboy]

Grijze Vos schreef op woensdag 10 februari 2010 @ 13:01:
[...]

Ik vind loopjes juist bij uitstek de plek om dit te doen.

C#:

List<NewsArticle> articles = News.GetArticles();
foreach(var article in articles)
{ // doe iets
}

Hartstikke leesbaar.
Hier declareer ik wel het type van de lijst, omdat die uit een externe functie komt.

Prima leesbaar inderdaad, maar waarom expliciet een List aanmaken?

Dan vind ik deze optie beter:

C#:

var articles = News.GetArticles();
foreach(NewsArticle article in articles)
{ // doe iets
}

Of als je articles toch niet meer nodig hebt misschien zelfs dit:

C#:

foreach(NewsArticle article in News.GetArticles())
{ // doe iets
}

[Grijze Vos]

.oisyn schreef op vrijdag 12 februari 2010 @ 00:12:
[...]

meer complexiteit.

Bedoel je computationele complexiteit? Want dat lijkt me nog steeds O(log n + k), waarbij k het aantal elementen is waarover je itereert. Nou ja, het is eigenlijk O(log n m*p), waarbij m*p=k.

RayNbow schreef op vrijdag 12 februari 2010 @ 00:26:
[...]

Momenteel is het praktische nut nog niet heel erg groot, maar dat komt omdat er nog weinig andere classes zijn die de LINQ operators implementeert. Standaard heb je alleen alle IEnumerable en IQueryable classes en sinds kort kun je spelen met Rx's IObservable classes. Nu kun je er nog mee wegkomen om 1 extra kopie te maken met alleen een andere type signature...

En het praktisch nut wordt ook niet groter. Als je zelf een Linq provider wilt schrijven is het de bedoeling dat je IQueryable implementeert (ik zei IEnumerable in mijn vorige post, maar ik bedoelde IQueryable.) Ik vind het perfect acceptabel dat die eis er is. Leuk dat je nu de wiskundige duaal hebt in de vorm van IObservable, maar welke interfaces verwacht je nog meer te implementeren die niet een van die twee kunnen implementeren?

Het is ook lastig te fixen, maar dat verandert weinig aan m'n mening dat C#'s type system niet erg krachtig is.

Ik was niet degene die die opmerking maakte over de kracht van C#'s type systeem, maar ik denk dat die poster bedoelde in vergelijking met andere imperatieve talen, niet in vergelijking met functionele talen. Je commentaar komt op mij over als functioneel fanboy-talk, om eerlijk te zijn.

[ Voor 67% gewijzigd door Grijze Vos op 12-02-2010 09:31 ]

[.oisyn]

RayNbow schreef op vrijdag 12 februari 2010 @ 00:26:
Misschien wel met het jargon dat C of C++ proggers gebruiken, waarin map dus blijkbaar refereert naar een datastructuur met de eigenschap dat de keys geordend zijn. Voor mij is een map conceptueel niets anders dan een afbeelding van keys naar values.

Hmmm idd, daar heb ik helemaal niet bij stilgestaan

Grijze Vos schreef op vrijdag 12 februari 2010 @ 09:20:
[...]

Bedoel je computationele complexiteit?

Nee, ik bedoel meer code complexiteit. Een dubbele loop.

[ Voor 49% gewijzigd door .oisyn op 12-02-2010 11:09 ]

[RayNbow]

Grijze Vos schreef op vrijdag 12 februari 2010 @ 09:20:
[...]

En het praktisch nut wordt ook niet groter. Als je zelf een Linq provider wilt schrijven is het de bedoeling dat je IQueryable implementeert (ik zei IEnumerable in mijn vorige post, maar ik bedoelde IQueryable.) Ik vind het perfect acceptabel dat die eis er is.

Die eis is er niet.

Leuk dat je nu de wiskundige duaal hebt in de vorm van IObservable, maar welke interfaces verwacht je nog meer te implementeren die niet een van die twee kunnen implementeren?

Kan jij Func<E,A> de IEnumerable<A> of IObservable<A> interface laten implementeren dan? Ik heb hier laten zien dat het de Select operator kan implementeren. SelectMany is trouwens ook geen probleem:

C#:

public static Func<E,B> SelectMany<E, A, B>(this Func<E, A> f, Func<A, Func<E, B>> g) 
{
    return e => g(f(e))(e);
}
public static Func<E, C> SelectMany<E, A, B, C>(
    this Func<E, A> f,
    Func<A, Func<E, B>> g,
    Func<A, B, C> h
)
{
    return e => h(f(e), f.Select(g)(e)(e));
}

// gebruik:
var res = (from x in (Func<int,int>)(e => e+1)
           from y in (Func<int, int>)(e => e+1)
           select x+y)(3); // levert [s]7[/]8 op (edit: typfout)

Dit is trouwens een voorbeeld waarbij de compiler de implementatie van de SelectMany's zelf zou moeten kunnen vinden. Immers, zowel (e -> a) -> (a -> (e -> b)) -> (e -> b) als (e -> a) -> (a -> (e -> b)) -> (a -> b -> c) -> (e -> c) zijn te bewijzen in de propositielogica.

[...]

Ik was niet degene die die opmerking maakte over de kracht van C#'s type systeem, maar ik denk dat die poster bedoelde in vergelijking met andere imperatieve talen, niet in vergelijking met functionele talen.

Extension methods laten alleen niet de kracht van een type system zien. Het laat eerder zien dat je wat syntactische suiker kunt toevoegen als je de regels uitbreidt waar je een methode kunt vinden.

Je commentaar komt op mij over als functioneel fanboy-talk, om eerlijk te zijn.

Is het verkeerd om abstractie hoog in het vaandel te hebben? Daarnaast, wat maakt higher-kinded generics "functioneel"?

[D-Raven]

RayNbow schreef op vrijdag 12 februari 2010 @ 13:10:

[...]

Is het verkeerd om abstractie hoog in het vaandel te hebben? Daarnaast, wat maakt higher-kinded generics "functioneel"?

Strict gezien blijft het een uitbreiding op het (OO gebaseerde) type systeem. Maar als je gaat kijken naar de mogelijkheden die deze "uitbreiding" je zal geven zullen veel mensen dit al snel als een feature in een functionele taal bestempelen. Puur omdat je niet gewend bent dit soort constructies te zien in .Net.

Komt op neer dat higher-kinded-generics je in staat stelt om meer "functioneel achtige" dingen te doen in een OO taal. Wellicht dat mensen het daarom als "functioneel" bestempelen.

[ Voor 13% gewijzigd door D-Raven op 12-02-2010 14:25 . Reden: verduidelijking ]

[.oisyn]

Er is niets functioneel aan. Het is generic programming. In C++ kan het overigens wel (behalve de select syntax natuurlijk). Wel weer jammer is overigens dat je in C++0x geen template parameters kunt deduceren aan de hand van een lambda, wat ik een beetje een gemiste kans vindt

[Alex)]

Ik gebruik var nooit. Als ik var tegenkom in de code van anderen, klik ik erop en laat ik ReSharper het type expliciet specificeren. Ik vind var's niet fijn werken, en met het oog op consistente code gebruik ik ook een expliciet type bij bijvoorbeeld Collections. Dan maar iets meer letters, IntelliSense (zeker de R#-versie) scheelt toch een hoop typwerk.

Zelfs het resultaat van LINQ-queries gooi ik in een strongly-typed variabele:

C#:

IEnumerable<Reservering> reserveringen = from Reservering r in GetReserveringen()
                                         where r.Id.ToString().StartsWith("42")
                                         select r;

Prachtig

[pedorus]

RayNbow schreef op vrijdag 12 februari 2010 @ 00:26:
Wat is dat voor redenatie? Als ik nu een IEnumerable<int> heb, maar ook een IObservable<int>, dan moet ik dus maar mijn addOne functie twee keer schrijven?

Nee, liefst niet als het logisch is om dezelfde functie op beide toe te passen. Ik ben zelf ook sterk voorstander om zo generiek mogelijke methodes te hebben. Als voorbeeld: in pedorus in "\[C#][discussie] Lekker veel var gebruiken?" staat een methode die alleen voor Lists werkt, maar generieker had gemoeten:

C#:

        public static void Put<TCol, TKey, TValue>(this IDictionary<TKey, TCol> d,
                TKey key, TValue value) 
            where TCol : ICollection<TValue>, new()
        {
            TCol elem;
            if (d.TryGetValue(key, out elem)) elem.Add(value);
            else d[key] = new TCol() { value };
        }

Dan hoef je voor een SortedList<TKey,HashSet<TValue>> niet opeens een andere functie te hebben.

Of stel je voor dat ik op een of andere manier die IObservable met een hamer bewerk totdat het in de vorm van IEnumerable past?

Ik vraag me af of er echt concrete voorbeelden zijn van functies die nuttig zijn op die beide types. Als dat zo is, hadden ze het liefst beiden eenzelfde interface gehad, waarbij ik ook nog links zie richting AOP om zoiets achteraf toe te voegen. AOP wordt nog niet in c# ondersteund vanwege potentiële havoc en nog niet duidelijk genoeg praktisch nut. Over deze ondersteuning:

quote: http://www.artima.com/intv/generics3.html

Bill Venners: So the type must either extend a class or implement interfaces.

Anders Hejlsberg: Yes. And we could have gone further. We did give thought to going further, but it gets very complicated. And it's not clear that the added complexity is worth the small yield that you get. If something you want to do is not directly supported in the constraint system, you can do it with a factory pattern. You could have a Matrix<T>, for example, and in that Matrix you would like to define a dot product method. That of course that means you ultimately need to understand how to multiply two Ts, but you can't say that as a constraint, at least not if T is int, double, or float. But what you could do is have your Matrix take as an argument a Calculator<T>, and in Calculator<T>, have a method called multiply. You go implement that and you pass it to the Matrix.

Ik volg je niet. Het gaat er niet om dat ik een Func<int,B> wil toepassen op ints, zoals je hierboven doet. Het gaat erom dat ik een functie wil kunnen toepassen op alle mogelijke functors, niet alleen op een select gezelschap onder de noemer IEnumerable<int>.

Het gaat erom dat jouw 2-regelige operatie op die class werkt, hoewel die class geen ?<int> is. Je hebt dan dus weer een nieuwe, losse implementatie nodig:

C#:

        public static IEnumerable<int> addOne(this TestSelect xs)
        {
            return from x in xs
                   select x + 1;
        }

Dit lijkt me niet iets dat het type-systeem van c# moet oplossen, maar meer een geval dat de class TestSelect bepaalde interfaces gewoon had moeten implementeren.

Mijn addOne is niets anders dan een simpel, kunstmatig voorbeeld om aan te tonen dat zonder higher-kinded polymorphism ik meerdere keren een functie moet schrijven, waarbij de body exact hetzelfde is en alleen de type signature verschilt.
[...]
...maar wanneer je zo'n extra kopie maakt, heb je je dan in feite jezelf niet herhaald? Is dat misschien niet net zo erg als de herhaling in "List<string> stringList = new List<string>();"?

Ik zit me af te vragen of een functie niet vaak ook hele andere functionaliteit krijgt heeft als twee classes niet dezelfde interface hebben. Als de naam dan niet meer klopt, dan is herhaling beter. Daarnaast zit je natuurlijk met afnemende meeropbrengsten. Het geval "List<string> stringList = new List<string>();" komt veel vaker voor, en -in mijn ogen- is daar nu een oplossing voor: var.

RayNbow schreef op vrijdag 12 februari 2010 @ 13:10:

C#:

           select x+y)(3); // levert 7 op

Het lijkt mij 8 (2*3+2), maar sowieso is het zonder concrete toepassingen mij niet helemaal duidelijk waarom je hier c# en linq voor wil gebruiken, en al helemaal niet waarom je een operatie op functies ook op IEnumerables wil toepassen.

Neverwinterx schreef op vrijdag 12 februari 2010 @ 00:28:
Ik vind het wat vreemd dat dit wordt aangehaald als een goed gebruik van var:

Java:

List<String> bad = new ArrayList<String>();
var good = new ArrayList<String>();

Een goed systeem (zoals in Java 7 zal komen) zou dit moeten kunnen doen:

Java:

List<String> best = new ArrayList<>();

Een wat uitgebreider voorbeeld:

Java:

Map<String, List<String>> anagrams = new HashMap<>();

Dat vermijdt ook de verbositeit, maar sleurt er niet iets obscuur als var bij.
(http://mail.openjdk.java....2009-February/000009.html)

Ik heb ook even naar deze link gekeken. Persoonlijk zie ik niet helemaal in wat er 'obscuur' is aan var. Daarnaast herhaal je nu List volgens interface=implementatie. Ik zie nog steeds niet in wat het grote voordeel daarvan is bij lokale variabelen. En ik vraag me af of het echt logisch is om aan de right-hand-side opeens informatie te hebben die niet op zichzelf staat. De '='-operator werkt zo 2 kanten op. Dit is niet perse waar in java omdat HashMap at run-time maar 1 implementatie heeft, maar c# heeft at run-time meerdere, aparte implementaties, bijvoorbeeld voor int, double en object. Dus nee, eigenlijk vind ik var mooier, omdat je dan maar 1x List hebt, en de '='-operator maar 1 kant op werkt.

Alex) schreef op vrijdag 12 februari 2010 @ 15:31:
Zelfs het resultaat van LINQ-queries gooi ik in een strongly-typed variabele:

Dat doe ik ook, door var te gebruiken. Hou je op jouw manier nog wel schermruimte over? En daarnaast: hoe zie je de consistentie met anonymous types waar dit niet bij kan?

[Alex)]

pedorus schreef op vrijdag 12 februari 2010 @ 16:00:
[...]

Dat doe ik ook, door var te gebruiken. Hou je op jouw manier nog wel schermruimte over? En daarnaast: hoe zie je de consistentie met anonymous types waar dit niet bij kan?

Var is in mijn ogen niet strongly-typed. Het mag het dan wel zijn, het ziet er gewoon niet zo uit en doet me alleen maar aan Javascript en PHP denken, daarom gebruik ik het niet. Op 1920x1200 heb ik wel genoeg ruimte

Ik vind het gewoon consistent als overal het type gespecificeerd staat... ik ben totnutoe nog geen types tegengekomen waarbij ik per sé 'var' moet gebruiken :-)

[.oisyn]

Het mag het dan wel zijn, het ziet er gewoon niet zo uit en doet me alleen maar aan Javascript en PHP denken, daarom gebruik ik het niet.

Tja, jouw persoonlijk probleem, en niet die van var

[pedorus]

Alex) schreef op vrijdag 12 februari 2010 @ 16:30:
Var is in mijn ogen niet strongly-typed. Het mag het dan wel zijn, het ziet er gewoon niet zo uit en doet me alleen maar aan Javascript en PHP denken, daarom gebruik ik het niet. Op 1920x1200 heb ik wel genoeg ruimte

offtopic:
Wil je nooit twee dingen naast elkaar zien dan?

Misschien toch ook eens F# proberen, als je bij var teveel richting Javascript/PHP denkt. Maar is het geen paradox dat je R# gebruikt om de boel uit te schrijven, terwijl de mensen achter Resharper dus zelf aanraden om dit juist niet te doen? Link uit de OP (emphasis theirs):

quote: http://resharper.blogspot...ing-implicitly-typed.html

Of course, you can hide this suggestion by using Options / Code Inspection / Inspection Severity, or by using Alt-Enter and selecting "Change severity" option. But what's the deal with implicitly typed locals, anyway? Using var keyword can significantly improve your code, not just save you some typing.

Ik vind het gewoon consistent als overal het type gespecificeerd staat... ik ben totnutoe nog geen types tegengekomen waarbij ik per sé 'var' moet gebruiken :-)

Misschien wordt het dan tijd voor interessantere code. Juist bij linq-queries zie ik het consistentie-oogpunt niet zo (en gebruik ik dus sowieso var); naar alle waarschijnlijkheid gebruiken verreweg de meeste programmeurs daarbij juist var, het is er tenslotte voor verzonnen. var en from/select zijn tegelijkertijd geïntroduceerd, dus waarom zou je de een wel gebruiken (niet consistent met oude code) en de ander niet (ivm consistentie)?

[RayNbow]

pedorus schreef op vrijdag 12 februari 2010 @ 16:00:
[...]

Ik vraag me af of er echt concrete voorbeelden zijn van functies die nuttig zijn op die beide types.

Die zijn er wel hoor...

C#:

// vul voor M iets in als bijv. IEnumerable of IObservable
M<A> Join(M<M<A>>);
M<List<A>> Sequence(List<M<A>>);
M<List<B>> MapM(Func<A, M<B>>, List<A>);
M<List<A>> FilterM(Func<A, M<bool>>, List<A>);
M<List<A>> ReplicateM(int, M<A>);
M<B> Ap(M<Func<A, B>, M<A>);
// etc...

Dit lijkt me niet iets dat het type-systeem van c# moet oplossen, maar meer een geval dat de class TestSelect bepaalde interfaces gewoon had moeten implementeren.

Het hele probleem is dus dat je het niet in interfaces kwijt kunt.

Ik zit me af te vragen of een functie niet vaak ook hele andere functionaliteit krijgt heeft als twee classes niet dezelfde interface hebben.

Klopt, de werkelijke functionaliteit hangt ook af van het concrete type. Desondanks zijn er wel bepaalde wetten (die niet door het type system worden gecontroleerd/geforceerd; ook niet in bijv. Haskell) waar je aan moet houden om een beetje zinnige implementaties van Select en SelectMany te kunnen schrijven.

Als de naam dan niet meer klopt, dan is herhaling beter.

Er zijn wel namen te verzinnen.

Daarnaast zit je natuurlijk met afnemende meeropbrengsten. Het geval "List<string> stringList = new List<string>();" komt veel vaker voor, en -in mijn ogen- is daar nu een oplossing voor: var.

True, en het is ook een aangename toevoeging aan de taal. Neemt niet weg dat ik graag higher-kinded generics in C# wil zien. Het is alleen een lastige kwestie. Zo is bijv. de syntax die ik voorstelde niet helemaal perfect en handig.

[...]
Het lijkt mij 8 (2*3+2),

Typfout van mij:p
(eig. een probleem van veelvuldig editen en vergeten om de gehele code naar de browser te copy/pasten )

maar sowieso is het zonder concrete toepassingen mij niet helemaal duidelijk waarom je hier c# en linq voor wil gebruiken,

Func<E, > wordt de Reader monad genoemd en representeert berekeningen die van een gemeenschappelijk omgeving (environment) lezen.

Over het gebruik van LINQ: het is een syntax voor monad comprehensions, dus waarom niet?

en al helemaal niet waarom je een operatie op functies ook op IEnumerables wil toepassen.

Bedoel je niet andersom? Waarom ik Select en SelectMany naast IEnumerables ook op functies wil toepassen?

[pedorus]

RayNbow schreef op vrijdag 12 februari 2010 @ 17:25:
True, en het is ook een aangename toevoeging aan de taal. Neemt niet weg dat ik graag higher-kinded generics in C# wil zien. Het is alleen een lastige kwestie. Zo is bijv. de syntax die ik voorstelde niet helemaal perfect en handig.
[...]
Over het gebruik van LINQ: het is een syntax voor monad comprehensions, dus waarom niet?

Ik heb inmiddels de belangrijkste man achter c# al gequote, maar deze wil ik je ook niet onthouden:

quote: http://blogs.msdn.com/wes...he-marvels-of-monads.aspx

If the word "continuation" causes eyes to glaze over, then the word "monad" induces mental paralysis.

Het zal dus nog wel even duren (of zelfs nooit gebeuren) voordat we hier grootse toevoegingen kunnen verwachten. Je ziet het ook al hoe hier op 'var' gereageerd wordt: veel programmeurs zijn tamelijk conservatief, zeker bij serieuzere code. Ik kan me nog herinneren dat generics in beta waren en ik voorstelde om ze in een subproject te gaan gebruiken: 'waarom zou je dat willen?' In 2008, toen R3 vroeg 'Even iets compleet anders: waarom is alles "var" bij jou?' dacht ik precies hetzelfde. Inmiddels begin ik dus meer in dezelfde richting als de R#-ontwikkelaars te denken als het om var gaat. Het nut van 'higher-kinded generics' bij praktische toepassingen ontgaat me nu nog steeds, maar bij var ben ik om.

Bedoel je niet andersom? Waarom ik Select en SelectMany naast IEnumerables ook op functies wil toepassen?

Dat is inderdaad een betere formulering.

[Phyxion]

Ik gebruik var nooit behalve bij Linq, ik vind het ontzettend onleesbaar, ik wil graag meteen zien welk type het is

[cfern]

Zijn er hier C# programmeurs met codeerafspraken op het werk die het gebruik van var aanmoedigen danwel verbieden? Aangezien niet iedereen gecharmeerd is van var, ben ik wel benieuwd hoe eventuele conflicten binnen teamverband worden aangepakt.

[Grijze Vos]

Wij zijn pas eigenlijk sinds kort overgestapt op .NET 3.5, aangezien ons belangrijkste product nog steeds 2.0 was. Binnenkort maar eens een keer discussieren om het gebruik van var in onze coding standards op te nemen.

[RayNbow]

pedorus schreef op zaterdag 13 februari 2010 @ 13:55:
Ik heb inmiddels de belangrijkste man achter c# al gequote, maar deze wil ik je ook niet onthouden:

[...]

Je laat nu net het belangrijkste weg:

quote: http://blogs.msdn.com/wes...he-marvels-of-monads.aspx

Perhaps, this is why some have begun inventing more benign names for monads.

Zelfs Simon Peyton-Jones (GHC developer; MS Research) is van mening dat monad een slechte naam is:

quote: http://www.dotnetrocks.com/text/0310/index11.html

Simon Peyton Jones:
Okay. The worst thing about monad is the name.

Richard Campbell:
They sound far worse than they are.

Simon Peyton Jones:
Yeah, that's why. The name is very off-putting because it comes from something mathematical. I'm on record as saying we should have called them warm, fuzzy things.

Het zal dus nog wel even duren (of zelfs nooit gebeuren) voordat we hier grootse toevoegingen kunnen verwachten. Je ziet het ook al hoe hier op 'var' gereageerd wordt: veel programmeurs zijn tamelijk conservatief, zeker bij serieuzere code.

Mjah, conservatisme zie je helaas in de gehele geschiedenis van de informatica terug.

Ik kan me nog herinneren dat generics in beta waren en ik voorstelde om ze in een subproject te gaan gebruiken: 'waarom zou je dat willen?'

Als een bepaalde feature nog in beta was, dan zou ik me wel kunnen voorstellen dat je het nog niet zou toepassen in een (sub)project.

In 2008, toen R3 vroeg 'Even iets compleet anders: waarom is alles "var" bij jou?' dacht ik precies hetzelfde. Inmiddels begin ik dus meer in dezelfde richting als de R#-ontwikkelaars te denken als het om var gaat.

Dat was dus een probleem van gewenning. Als je gewend bent om bij elke variabele een expliciete typeannotatie te zien, dan moet je leren die gewenning ongedaan te maken.

Het nut van 'higher-kinded generics' bij praktische toepassingen ontgaat me nu nog steeds, maar bij var ben ik om.

Misschien zijn er twee dingen nodig om 't nut te kunnen inzien van higher-kinded generics. Ten eerste is de notatie. Je moet jezelf wel makkelijk kunnen uitdrukken in een taal en ook ermee kunnen spelen (i.e., uitvoerbare code). Relevant stukje conversatie op IRC een tijdje terug:

quote: IRC

<RayNbow> <luite> geeft trouwens wel aan hoeveel notatie uitmaakt <-- hoe bedoel je precies?
<RayNbow> als de notatie te lastig wordt... dat mensen dan minder geneigd zijn om 't als bruikbaar te zien?
<luite> ja idd, als notatie 'natuurlijk' is ben je veel sneller geneigd een abstractie te accepteren en als bruikbaar te zien

Ten tweede is het belangrijk om de juiste patronen te kennen en kunnen herkennen. Als je bijvoorbeeld inziet dat iets zich gedraagt als een monad, dan weet je dat je in C# de LINQ syntax kunt gebruiken.

Ter illustratie, probabilistische netwerken vormen een monad en we kunnen dus de LINQ syntax gebruiken. Het voorbeeld dat ik ga bespreken heb ik uit deze (redelijk toegankelijke) talk, die het op zijn beurt van Wikipedia heeft:

quote: http://en.wikipedia.org/wiki/Bayesian_network

Suppose that there are two events which could cause grass to be wet: either the sprinkler is on or it's raining. Also, suppose that the rain has a direct effect on the use of the sprinkler (namely that when it rains, the sprinkler is usually not turned on). Then the situation can be modeled with Bayesian network. All three variables have two possible values T (for true) and F (for false).

De kans dat het gras nat is kan met het volgende diagram worden weergegeven:


(klikbaar voor iets grotere versie)

De pijlen in dit diagram laten zien hoe de informatie stroomt. Uit de stochast "Rain" vloeit de informatie of het wel of niet regent en draagt in het diagram het label r. Zoals je kunt zien bereikt deze informatie de stochasten "Sprinkler" en "Grass wet". Op dezelfde wijze stroomt er informatie van "Sprinkler" naar "Grass wet". De informatie of het gras nat is vloeit van "Grass wet" uit het gehele diagram.

We kunnen ook de vraag stellen: "wat is de kans dat het regent, gegeven het feit dat gras nat is?". Deze vraag wordt in het volgende diagram worden weergegeven:



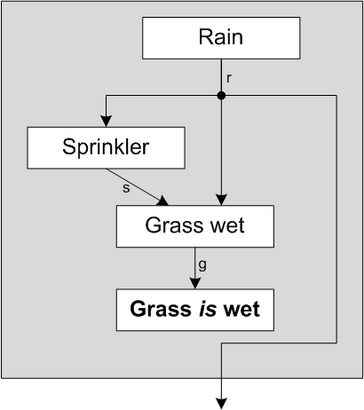
Het diagram is vrijwel hetzelfde als voorheen, alleen nu voegen we een bewering toe dat de informatie van "Grass wet" waar moet zijn (="Grass is wet") en i.p.v. of het gras nat is laten we de informatie uit "Rain" naar buiten vloeien.


Deze diagrammen kun je 1-op-1 vertalen naar code. We liften eerst de booleans true en false naar een rijker type. Dit scheelt namelijk straks wat typwerk:

C#:

static Prob PFalse = new Prob(false);
static Prob PTrue = new Prob(true);

Vervolgens implementeren we de kanstabellen:

C#:

static Prob Rain()
{
    return 0.2 * PTrue + 0.8 * PFalse;
}

static Prob Sprinkler(bool raining)
{
    return
        !raining  ?  0.40 * PTrue + 0.60 * PFalse  :
        raining   ?  0.01 * PTrue + 0.99 * PFalse  :
        null;
}

static Prob GrassWet(bool sprinkler, bool raining)
{
    return
        !sprinkler  &&  !raining  ?  PFalse                        :
        !sprinkler  &&  raining   ?  0.80 * PTrue + 0.20 * PFalse  :
        sprinkler   &&  !raining  ?  0.90 * PTrue + 0.10 * PFalse  :
        sprinkler   &&  raining   ?  0.99 * PTrue + 0.01 * PFalse  :
        null;
}

(Deze code kan korter, maar dan mis je de tabelstructuur)

Uiteindelijk kun je elk van de twee diagrammen beschrijven met een LINQ query:

C#:

static void Main(string[] args)
{
    var grasswet = from r in Rain()
                   from s in Sprinkler(r)
                   from g in GrassWet(s, r)
                   select g;
    
    var diditrain = from r in Rain()
                    from s in Sprinkler(r)
                    from g in GrassWet(s, r)
                    where g
                    select r;
    
    Console.WriteLine(grasswet);  // <0,44838:True, 0,55162:False>
    Console.WriteLine(diditrain); // <0,16038:True, 0,288:False>
    Console.WriteLine(diditrain / diditrain.Norm1()); // <0,357687675632276:True, 0,642312324367724:False>
    Console.ReadKey();
}

De from-clauses labelen de informatie die uit een stochast stroomt, zodat we deze informatie aan andere stochasten kunnen doorgeven. Met een where-clause kunnen we "gegeven het feit dat..." modeleren en met select-clause kunnen we opgeven welke informatie uit het diagram vloeit.

[ Voor 0% gewijzigd door RayNbow op 28-03-2011 18:16 . Reden: link fix ]

[pedorus]

RayNbow schreef op maandag 22 februari 2010 @ 00:17:
De from-clauses labelen de informatie die uit een stochast stroomt, zodat we deze informatie aan andere stochasten kunnen doorgeven. Met een where-clause kunnen we "gegeven het feit dat..." modeleren en met select-clause kunnen we opgeven welke informatie uit het diagram vloeit.

Ik heb het even uitgeprobeert met de code van http://tinypaste.com/d8f77 en het werkt goed inderdaad. Ik denk enkel dat je voor praktische toepassingen dit niet direct in c# wilt hebben, omdat je dan ongeveer vanuit je UI steeds de c#-compiler moet gaan aanroepen ofzo. Je zal meestal een willekeurig netwerk willen kunnen doorrekenen in je programma, niet eentje waarvan de attributen en relaties al vast staan (en als dit niet zo is, zul je waarschijnlijk juist nog specifiekere code willen hebben).

De code op tinypaste is trouwens een mooi voorbeeld van dat de duidelijkheid van var niet perse door de kortheid komt. Ze doen daar exact hetzelfde als wat jij doet:

C#:

            var grasswet = from r in Rain()
                           from s in Sprinkler(r)
                           from g in Grass(s, r)
                           select g;

Terwijl het daar met typenaam korter is, maar in mijn ogen minder leesbaar/handig:

C#:

            V grasswet = from r in Rain()
                         from s in Sprinkler(r)
                         from g in Grass(s, r)
                         select g;

[RayNbow]

pedorus schreef op maandag 22 februari 2010 @ 20:47:
[...]

Ik heb het even uitgeprobeert met de code van http://tinypaste.com/d8f77 en het werkt goed inderdaad.
[...]
De code op tinypaste is trouwens een mooi voorbeeld van dat de duidelijkheid van var niet perse door de kortheid komt. Ze doen daar exact hetzelfde als wat jij doet:

C#:

            var grasswet = from r in Rain()
                           from s in Sprinkler(r)
                           from g in Grass(s, r)
                           select g;

Terwijl het daar met typenaam korter is, maar in mijn ogen minder leesbaar/handig:

C#:

            V grasswet = from r in Rain()
                         from s in Sprinkler(r)
                         from g in Grass(s, r)
                         select g;

Die tinypaste is een oude versie van m'n code. Op een gegeven moment vond ik Prob een betere naam dan alleen V van vector.

Edit: hier is een paste van de recentste versie.

Ik denk enkel dat je voor praktische toepassingen dit niet direct in c# wilt hebben, omdat je dan ongeveer vanuit je UI steeds de c#-compiler moet gaan aanroepen ofzo. Je zal meestal een willekeurig netwerk willen kunnen doorrekenen in je programma, niet eentje waarvan de attributen en relaties al vast staan

De diagrammen waren een visualisatie van het voorbeeld, maar ook in zekere zin van de code. Als je een GUI wilt bouwen waarin de gebruiker zelf het netwerk visueel kan construeren, dan zal je waarschijnlijk o.a. elke node door een object laten representeren.

Maar zelfs in die andere representatie blijft de monadische structuur bestaan.

(en als dit niet zo is, zul je waarschijnlijk juist nog specifiekere code willen hebben).

Als alles vast staat kun je eigenlijk aan constant-folding doen.

[ Voor 4% gewijzigd door RayNbow op 22-02-2010 21:39 ]

[Ankona]

Zo even een oud topic onder het stof vandaan gehaald en een rotschop gegeven.

We zijn inmiddels een jaar of 10 verder maar deze discussie voer ik op mijn werk nog steeds vaak. Zelf ben ik absoluut geen voorstander van het gebruik van var anders dan voor anonymous types. Microsoft adviseert het gebruik ervan mits aan de assignment direct te zien is om welk type het gaat. (dus aanroepen van een constructor, niet bij het aanroepen van een functie)
Resharper maakt er helemaal een puinhoop van, die adviseert het altijd met als gevolg onleesbare code (je weet niet waar je mee aan het werk bent) die gevoelig is voor onverwacht gedrag (als die functie aangepast wordt kan het zo zijn dat de compiler het nog steeds prima vindt maar je werkt ineens met een heel ander type)

Spottend zeg ik vaak dat var ideaal is voor developers die geen idee hebben wat ze aan het doen zijn.

Sommige collega's noemen nog als voordeel dat als je een rijtje declaraties hebt, ze met var zo mooi recht uitgelijnd staan. Tja, dan schrijf je meestal slechte code met veel te veel responsibility.

Op zich kan ik nog wel redelijk leven met de guideline van Microsoft al ben ik niet overtuigd van de voordelen. (Ok, bij lange type namen kan het wat lange regels met herhaling van zetten opleveren. Dan valt er wel wat voor var te zeggen - uit consistentie oogpunt verkies ik het dan om ook in die gevallen geen var te gebruiken maar dat is mijn voorkeur.)

Weet iemand de echte reden waarom Microsoft en zeker Resharper zulke fans zijn van var? Sommige teams leunen blind op deze aanbevelingen wat discussies erg lastig maakt.

[RayNbow]

Ankona schreef op dinsdag 15 september 2020 @ 23:28:
Weet iemand de echte reden waarom Microsoft en zeker Resharper zulke fans zijn van var?

Wanneer is het echt belangrijk om te weten wat het type is van een variabele? Het idee is dat een variabelenaam al beschrijvend genoeg moet zijn.

[Ankona]

De variabele naam is vooral beschrijvend naar het domein toe, niet naar de implementatie. Ik ben het wel met je eens dat goede code makkelijker leest, zeker ook als namen goed gekozen zijn.
Maar wanneer lees je nou je code? Vooral als je bugs aan het oplossen bent, dan is het erg plezierig om een goed beeld van de implementatie te hebben om te begrijpen waarom het ander gedrag vertoont dan je verwacht.
En tijdens het schrijven zelf vind ik het ook wel handig. Ik werk nu in een team waar men afgesproken heeft dat alles var MOET zijn. Ik ontwikkel dat alles expliciet en vlak voor de code review refactor ik de boel pas naar var.

[Cyphax]

Ankona schreef op woensdag 16 september 2020 @ 07:26:
De variabele naam is vooral beschrijvend naar het domein toe, niet naar de implementatie.

Als je bekend bent met dat domein, dan weet je toch alsnog wat iets, is als de naamgeving maar beschrijvend is?
Ik moest in het begin ook niets hebben van dat 'var' overal, maar over de jaren heen is het ingeburgerd en is het wel prettig. Het maakt in mijn ervaringen vaak niet zo heel veel uit wat iets precies is. Het is misschien lastig te pinpointen maar ik kan me niet herinneren dat ik in de afgelopen jaren eens heb gedacht "damnit stond hier maar niet 'var'".

[Ankona]

Cyphax schreef op woensdag 16 september 2020 @ 07:39:
[...]

Als je bekend bent met dat domein, dan weet je toch alsnog wat iets, is als de naamgeving maar beschrijvend is?

Tenzij daar juist de fout zit. Bijvoorbeeld omdat een int gebruikt is waar het een double had moeten zijn. Of nog een decimal waar je jaren geleden had besloten bedragen (oid) uit te drukken in een eigen value type.

Verder heb je soms (ik werk nu aan een grote technische applicatie) te maken met zeer complexe model structuren. Dan ben je ook al snel het overzicht kwijt tenzij je in de naamgeving precies vast gaat leggen wat je eigenlijk aan de declaratie al had moeten kunnen zien.

Kortom, zat situaties waar het niet echt nodig hoeft te zijn, maar in mijn ogen geen situaties waarin het een voordeel biedt om var te gebruiken. En nog genoeg situaties waarin expliciete declaraties toch wel plezieriger zijn. (naar mijn mening dan)

[Cyphax]

Ankona schreef op woensdag 16 september 2020 @ 07:47:
[...]

Tenzij daar juist de fout zit. Bijvoorbeeld omdat een int gebruikt is waar het een double had moeten zijn. Of nog een decimal waar je jaren geleden had besloten bedragen (oid) uit te drukken in een eigen value type.

Over het algemeen komen die waarden uit functies met een return type. Imho de verkeerde plek om je daar zorgen over te maken. Hangt mogelijk ook af van het type applicatie waar je in zit, hoewel ik zo niet iets kan bedenken.

Verder heb je soms (ik werk nu aan een grote technische applicatie) te maken met zeer complexe model structuren. Dan ben je ook al snel het overzicht kwijt tenzij je in de naamgeving precies vast gaat leggen wat je eigenlijk aan de declaratie al had moeten kunnen zien.

Ja, nou, ik doe al jaren hetzelfde en ik ben nooit het overzicht kwijt. Daarom zal het wel persoonlijke voorkeur zijn met name. Maar het is imho vooral fout om iets wat niet jouw voorkeur heeft fout te noemen. Dan doe je anderen tekort vind ik.

Kortom, zat situaties waar het niet echt nodig hoeft te zijn, maar in mijn ogen geen situaties waarin het een voordeel biedt om var te gebruiken. En nog genoeg situaties waarin expliciete declaraties toch wel plezieriger zijn. (naar mijn mening dan)

Dat geeft ook niet, het is ook niet erg, het is vooral goed om er enigszins bij stil te staan uiteindelijk, dan heb je altijd een weloverwogen keuze en over smaak en voorkeur valt ook niet te twisten.

[ Voor 3% gewijzigd door Cyphax op 16-09-2020 07:54 ]

[RayNbow]

Ankona schreef op woensdag 16 september 2020 @ 07:26:
Maar wanneer lees je nou je code? Vooral als je bugs aan het oplossen bent, dan is het erg plezierig om een goed beeld van de implementatie te hebben om te begrijpen waarom het ander gedrag vertoont dan je verwacht.

Maar voldoen de types die in de type-signature van je functie staan dan niet?

Ankona schreef op woensdag 16 september 2020 @ 07:47:
[...]

Tenzij daar juist de fout zit. Bijvoorbeeld omdat een int gebruikt is waar het een double had moeten zijn.

Dat lijkt me een slecht voorbeeld. Een compiler zal een type-error geven omdat een double niet impliciet om te zetten is naar een int.

[Black Eagle]

Ikzelf gebruik var voor alle complex types. Mensen die geen var willen gebruiken zie ik echt als die oude developers die te stug zijn om zich aan te passen. Elke editor laat het type zien met een mousehover en als je duidelijke namen kiest is al duidelijk wat voor type het is.

[RayNbow]

Laten we anders wat voorbeelden plaatsen. Hier is een stukje code dat var gebruikt:

C#:

// Read TIFF
using var tif = Tiff.Open(sourceImagePath, "r");
var w = tif.GetField(TiffTag.IMAGEWIDTH)[0].ToInt();
var h = tif.GetField(TiffTag.IMAGELENGTH)[0].ToInt();
var buf = new int[w * h];
tif.ReadRGBAImageOriented(w, h, buf, Orientation.TOPLEFT);

// Convert to BGR:
using var mat = new Mat<Vec4b>(h, w, buf);
using var matBGR = new Mat<Vec3b>();
Cv2.CvtColor(mat, matBGR, ColorConversionCodes.RGBA2BGR);

WriteResult(outputPath, matBGR, someOtherArgumentsThatDontMatterRightNow);

Wordt dit stukje code leesbaarder als we de types van tif, w, h, buf, mat en matBGR uitschrijven?

[Ankona]

RayNbow schreef op woensdag 16 september 2020 @ 07:54:
[...]

Maar voldoen de types die in de type-signature van je functie staan dan niet?
[...]
[...]

Dat lijkt me een slecht voorbeeld. Een compiler zal een type-error geven omdat een double niet impliciet om te zetten is naar een int.

Dat is nou net de grap, een var past zich automagisch aan waardoor de compiler het vaak wel ok vindt. Bij expliciete declaratie zou je wel gealarmeerd worden door de compiler.

[jessy100]

MBV schreef op dinsdag 9 februari 2010 @ 14:47:

offtopic:
viel mij ook al op ja. Heeft in deze context toch geen enkel nut, en kan toch ook voor een lagere performance zorgen? Los daarvan haal je alle voordelen van een strongly typed language weg, ga dan lekker ironPython gebruiken als je in .NET wilt spelen

Ik stoor me echt ernorm aan deze reactie in de OP. Lagere performance? hoe kom je er bij? Tijdens het omzetten naar IL code wordt var gewoon omgezet naar zijn expliciete type.. Voordelen van een strongly typed language bijven ook gewoon bestaan..

Iets met klok en klepel.

Overigens vind ik @pedorus zijn gebruik van var precies zoals het hoort. In mijn team zijn anti-var mensen vooral de wat ouderen die opgegroeid zijn zonder..

[Cyphax]

Ankona schreef op woensdag 16 september 2020 @ 08:31:
[...]

Dat is nou net de grap, een var past zich automagisch aan waardoor de compiler het vaak wel ok vindt.

Het is in de praktijk vaker wel dan niet okee. Ik geef veel interfaces door, als parameter bijvoorbeeld. Wat de instantie dan uiteindelijk wordt maakt me eigenlijk niet uit. Ik wil een collectie, dus ik vraag om een IEnumerable (mits ik me daartoe beperk, gewoon een foreach loopje bijvoorbeeld) als parameter of return type van een functie. Of er dan een List uitkomt of iets anders dat IEnumerable maar implementeert vind ik dat goed genoeg.
Natuurlijk is dat niet van toepassing bij strings en integers, maar ik besteed daar in de praktijk toch minder tijd aan blijkbaar. Anders zou ik er persoonlijk steeds tegenaan gelopen zijn. En een goede naamgeving is daarin voor mij meestal genoeg om niet in de war te raken.

[ Voor 4% gewijzigd door Cyphax op 16-09-2020 08:41 ]

[RobIII]

Ankona schreef op woensdag 16 september 2020 @ 07:26:
Maar wanneer lees je nou je code?

Uh, vaker dan je 't schrijft. Een regel code kun je maar één keer schrijven. Aangenomen dat je 'm dan ook meteen leest is 't 1:1 en vanaf dat punt wordt 't lezen alleen maar vaker en 't schrijven blijft 1.

quote: https://devblogs.microsof...hing/20070406-00/?p=27343

Code is read much more often than it is written, so plan accordingly.

Ik sta ook firm in "kamp var" (itt tot past self ).

C#:

DateTimeOffset date = DateTimeOffset.Now;
ApplicationRepositoryFactory repofact = new ApplicationRepositoryFactory(...);
Customer cust = repo.GetCustomerById(123);

//vs

var date = DateTimeOffset.Now;
var repofact = new ApplicationRepositoryFactory(...);
var cust = repo.GetCustomerById(123);

Zelfs zonder IDE is hier prima uit te komen. Er zijn best wel gevallen waar 't misschien niet altijd 100% duidelijk welk (afgeleid) type je terugkrijgt, maar niets wat een commentje of op die ene plek een expliciete declaratie of cast niet oplost.

C#:

var student = (IStudent)schoolRepo.GetPersonById(123);

[ Voor 5% gewijzigd door RobIII op 16-09-2020 10:42 ]

[AtleX]

In C#9 kan je met target typed new expressions wel kortere regels schrijven zonder var te vermijden. Bijvoorbeeld:

C#:

MemoryStream ms = new();

Ik weet nog niet zo goed wat ik er van vind, ik werk pas een paar weken met C#9 dus moet nog voor mezelf bepalen wanneer ik var fijner vind en wanneer target typed new expressions. Tot nu toe, pre C#9, zit ik nogal in Kamp Var. Het is veel makkelijker met refactoring en ik vind het makkelijker leesbaar ook.

[ Voor 4% gewijzigd door AtleX op 16-09-2020 08:54 ]

[Ankona]

RobIII schreef op woensdag 16 september 2020 @ 08:43:
[...]

Uh, vaker dan je 't schrijft. Een regel code kun je maar één keer schrijven. Aangenomen dat je 'm dan ook meteen leest is 't 1:1 en vanaf dat punt wordt 't lezen alleen maar vaker en 't schrijven blijft 1.

Klopt, de vraag was ook meer retorisch. Uit onderzoek blijkt dat de developer gemiddeld 5 keer zoveel tijd kwijt is met het lezen van zijn eigen code dan met het schrijven. (Daarom is wat meer tijd steken in het schrijven van code en geen vage afkortingen etc gebruiken ook gewoon tijdwinst. )

Maar wat ik bedoelde met de vraag is vooral het wanneer. Vaak als het nodig is om de implementatie goed te begrijpen om iets op te lossen of aan te passen. Niet zozeer om het globale functionele doel te begrijpen. (Daarvoor zou de methode naam voldoende moeten zijn)

[Rub3s]

Ankona schreef op dinsdag 15 september 2020 @ 23:28:
Spottend zeg ik vaak dat var ideaal is voor developers die geen idee hebben wat ze aan het doen zijn.

Je kan de discussie ook andersom voeren: Wat heb jij tegen var?

Zelf vind ik het gewoon minder typewerk. Ik typ al genoeg.

[RayNbow]

AtleX schreef op woensdag 16 september 2020 @ 08:47:
In C#9 kan je met target typed new expressions wel kortere regels schrijven zonder var te vermijden. Bijvoorbeeld:

C#:

MemoryStream ms = new();

Of je nu MemoryStream ms = new(); of var ms = new MemoryStream (); schrijft is om het even. In beide gevallen schrijf je het type maar 1x op. De nieuwe syntax is vooral handig voor fields in een class waarin var niet mogelijk is.

Ankona schreef op woensdag 16 september 2020 @ 08:31:
[...]

Dat is nou net de grap, een var past zich automagisch aan waardoor de compiler het vaak wel ok vindt. Bij expliciete declaratie zou je wel gealarmeerd worden door de compiler.

Kom eens met een concreet voorbeeld?

Kijk, ik snap dat het volgende een type-error is:

C#:

int result = someDouble();

En het volgende niet:

C#:

var result = someDouble();

Maar de tweede variant zal alsnog een type-error opleveren zodra je result ergens op een plek gebruikt waar een int verwacht wordt.

[Woy]

RobIII schreef op woensdag 16 september 2020 @ 08:43:

C#:

var student = (IStudent)schoolRepo.GetPersonById(123);

Ik moet zeggen dat ik een dergelijke cast alleen om te zorgen dat de var het juiste type krijgt wel lelijk vind, dan gebruik ik op die plek liever een expliciete declaratie.

[RobIII]

Woy schreef op woensdag 16 september 2020 @ 09:49:
[...]

Ik moet zeggen dat ik een dergelijke cast alleen om te zorgen dat de var het juiste type krijgt wel lelijk vind, dan gebruik ik op die plek liever een expliciete declaratie.

Was een beetje een geforceerd voorbeeld. Eens dat een expliciete declaratie dan mooier is.

RobIII schreef op woensdag 16 september 2020 @ 08:43:
of op die ene plek een expliciete declaratie of cast niet oplost.

[whoami]

AtleX schreef op woensdag 16 september 2020 @ 08:47:
In C#9 kan je met target typed new expressions wel kortere regels schrijven zonder var te vermijden. Bijvoorbeeld:

C#:

MemoryStream ms = new();

Ik weet nog niet zo goed wat ik er van vind, ik werk pas een paar weken met C#9 dus moet nog voor mezelf bepalen wanneer ik var fijner vind en wanneer target typed new expressions. Tot nu toe, pre C#9, zit ik nogal in Kamp Var. Het is veel makkelijker met refactoring en ik vind het makkelijker leesbaar ook.

Wat hier gebeurd is eigenlijk het omgekeerde van `var`

code:

var ms = new MemoryStream();

vind ik dan beter.

[ Voor 1% gewijzigd door whoami op 16-09-2020 09:52 . Reden: code-tags ipv markdown style code ]

[CodeCaster]

RayNbow schreef op woensdag 16 september 2020 @ 09:36:
[...]
... zal alsnog een type-error opleveren zodra je result ergens op een plek gebruikt waar een int verwacht wordt.

Tenzij de code erna gaat rekenen. Dan gebruik ik liever wel expliciete types, om te zien of er ergens ineens integer division gaat plaatsvinden.

Ik ben benieuwd of die nieuwe new()-syntax ook genest werkt? Dus:

C#:

Dictionary<string, Foo<Bar>> dict = new()
{
    { "baz", new(42) }, // instead of new Foo<Bar>(42)
    { "qux", new(21) },
};

[Hydra]

Ik gebruik zelf geen C# maar Kotlin, nu ongeveer 2 jaar full time. Kotlin heeft ook var/val. Ook in de Java wereld speelt deze discussie, met argumenten als dat de code onleesbaar wordt. M.i. is dit een compleet non-issue, integendeel: var/val dwingt je eerder om goede variabele namen te kiezen.

Mensen 'doen' alsof code er meestal zo uitziet:

code:

List<Person> persons = someService.findByName("Foo");
persons.doSomething();

Maar meestal is het zo iets:

code:

List<Person> persons = someService.findByName("Foo");

//heel veel regels code

persons.doSomething();

Daar is er een flinke afstand tussen de declaratie van het persons object, en het gebruik ervan. Dus er is echt geen groot verschil, m.i. is dat 'code lezen' een non-argument. Dat is ook mijn ervaring na 2 jaar full time Kotlin; de code wordt er absoluut niet slechter leesbaar door. Je hebt juist minder visuele overhead en je wordt meer gedwongen goeie namen te gebruiken.

[Cyphax]

Hydra schreef op woensdag 16 september 2020 @ 10:03:


Daar is er een flinke afstand tussen de declaratie van het persons object, en het gebruik ervan.

Ik zou dan die afstand verkleinen, maakt je method ws al een stuk leesbaarder los van of je var gebruikt of niet.

[RayNbow]

whoami schreef op woensdag 16 september 2020 @ 09:52:
[...]


Wat hier gebeurd is eigenlijk het omgekeerde van `var`

code:

var ms = new MemoryStream();

vind ik dan beter.

Maar dat werkt niet als veld-declaratie, vandaar de nieuwe syntax.

CodeCaster schreef op woensdag 16 september 2020 @ 09:59:
[...]

Tenzij de code erna gaat rekenen. Dan gebruik ik liever wel expliciete types, om te zien of er ergens ineens integer division gaat plaatsvinden.

Maar in welke situatie met var zal dit voorkomen? Dit zal alleen gebeuren als het resultaat ergens al een int was en je dus niet hebt omgezet naar een double.

Ik ben benieuwd of die nieuwe new()-syntax ook genest werkt? Dus:

C#:

Dictionary<string, Foo<Bar>> dict = new()
{
    { "baz", new(42) }, // instead of new Foo<Bar>(42)
    { "qux", new(21) },
};

Blijkbaar?

C#:

using System;
using System.Collections.Generic;

namespace csharp9test
{
    class Foo<T> {
        public int X { get; set; }
        public Foo(int x) 
        {
            X = x;
        }
    }
    
    class Bar {}
    
    class Program
    {
        static void Main(string[] args)
        {
            Dictionary<string, Foo<Bar>> dict = new()
            {
                { "baz", new(42) }, // instead of new Foo<Bar>(42)
                { "qux", new(21) },
            };

            Console.WriteLine($"Hello World! {dict["baz"].X}");
        }
    }
}

C:\tmp\csharp9test> dotnet run
Hello World! 42

Edit: Dit werkt ook:

C#:

var dict = new Dictionary<string, Foo<Bar>>()
{
    { "baz", new(42) }, // instead of new Foo<Bar>(42)
    { "qux", new(21) },
};

[ Voor 5% gewijzigd door RayNbow op 16-09-2020 10:21 ]

[ThomasG]

Rub3s schreef op woensdag 16 september 2020 @ 09:27:
[...]



Je kan de discussie ook andersom voeren: Wat heb jij tegen var?

Zelf vind ik het gewoon minder typewerk. Ik typ al genoeg.

Minder typewerk is niet echt een argument om var te gebruiken, want dat is een kwestie van een betere IDE gebruiken Ik typ zelf altijd de definitie, en laat de IDE met een toetsencombinatie de declaratie genereren. Dat scheelt een hoop typen, omdat de naam van de variabele 9 van de 10 keer goed is (wordt afgeleid van de methode naam en/of return value).

[Ankona]

RayNbow schreef op woensdag 16 september 2020 @ 09:36:

[...]

Kom eens met een concreet voorbeeld?

Het eerste waar ik dan meteen aan denk is het gedrag van operators op numerieke types. Met name delen is bij integers anders dan bij floating point types.

Verder kan het handig zijn bij primitieven om te zien of ze wel of niet nullable zijn. Dit zijn eigenlijk de eerste redelijk normale voorbeelden die me zo te binnen schieten. Meer geforceerde voorbeelden zijn als een return value van een functie verandert maar wel (een aantal) gelijknamige members heeft.

Maar terug op het meer algemene. Natuurlijk, ik heb mijn voorkeuren en het is goed om zelf ook regelmatig in de spiegel te kijken. Zeker als je merkt dat je tegen een stroom in zwemt. (toen var geïntroduceerd werd dook ik er ook als een jonge hond op om het te pas en te onpas te gebruiken, later ben ik steeds meer overtuigd geraakt dat het niets toevoegt en juist soms zaken onduidelijker of fout gevoeliger maakt )
Ik ben ervan overtuigd dat je in beide stijlen goede code kunt schrijven. Technisch maakt het helemaal niets uti voor de compiler (in IL wordt het hetzelfde dus verwacht geen performance argumenten)

Ik mis eigenlijk vooral de echte steekhoudende argumenten om informatie over de te gebruiken types af te willen schermen.

Wat betreft de leesbaarheid is het ook een stuk gewenning. Ik vind het plezierig dat een declaratie altijd begint met het type. Dan hoef ik niet te kijken naar waar het vandaan komt als ik alleen in het gedrag en niet in de instance zelf geïnteresseerd ben. Gewoon links in de regel staat dan wat ik wil weten. (maar dit is natuurlijk ook voor een groot deel net wat je gewend bent. Echter, afhankelijk zijn van je tooling om code te kunnen begrijpen vind ik nooit een goed uitgangspunt)

[AtleX]

whoami schreef op woensdag 16 september 2020 @ 09:52:
[...]


Wat hier gebeurd is eigenlijk het omgekeerde van `var`

code:

var ms = new MemoryStream();

vind ik dan beter.

Ja klopt. En ook eens. Al zijn target typed new expressions wel handig in static readonly fields of properties. Dat kunnen soms lange regels zijn en nu worden met target typed new expressions wat korter.

[RayNbow]

@Ankona: Met een concreet voorbeeld bedoelde ik een programma (of deel ervan) die het probleem waar je (met var) tegenaan loopt illustreert.

[Ankona]

RayNbow schreef op woensdag 16 september 2020 @ 10:36:
@Ankona: Met een concreet voorbeeld bedoelde ik een programma (of deel ervan) die het probleem waar je (met var) tegenaan loopt illustreert.

Fijn, dat je dat bedoelt maar het issue is zo ook wel duidelijk. Mijn productie code van onder NDA met de klanten dus die kan ik niet delen en anders zou ik een voorbeeld in elkaar moeten knutselen naar het probleem toe. Iets wat niets toevoegt. (En een stuk concrete code doorspitten om in een regel iets te herkennen wat je met een simpele beschrijving ook kunt duiden voegt ook weinig toe)

[Grijze Vos]

Ik denk dat het vooral smaak is. Mensen lezen nou eenmaal code anders. Ik heb ook collega's gehad die code moesten herschrijven voordat ze in staat waren de code te begrijpen. (Ok granted, deze collega's werken nu niet meer bij ons.)

Ankona schreef op dinsdag 15 september 2020 @ 23:28:
Spottend zeg ik vaak dat var ideaal is voor developers die geen idee hebben wat ze aan het doen zijn.

HIer zou ik dan weer terug op willen reageren door te zeggen dat als het wel of niet aanwezig zijn van var de leesbaarheid dermate beinvloed, dat dan je code gewoon slecht gestructureerd is. Als jij functies hebt van 5-10 regels code met iets van 2-3 variabelen in gebruik, dan maakt het echt geen drol meer uit.

Misschien moet iemand gewoon eens wat tijd investeren in een VS plugin die die var declaraties gewoon live vertaald naar de onderliggende type def. Wellicht zelfs gewoon met een keyboard shortcut om snel te togglen oid.

[Ankona]

Maar dan niet alleen in Visual Studio, ook je code review tooling moeten dat dan gaan ondersteunen. Ik wil voor een code review liever niet de branch ook nog lokaal in VS openen. Ik wil de code gewoon zelf begrijpen.

[Hydra]

Cyphax schreef op woensdag 16 september 2020 @ 10:11:
Ik zou dan die afstand verkleinen, maakt je method ws al een stuk leesbaarder los van of je var gebruikt of niet.

Dat is het punt niet

[Sissors]

Nu ben ik geen professioneel programmeur, en is mijn ervaring vooral in de embedded wereld, maar ik vind code die allemaal gebaseerd is op var of het equivalent in een andere taal veel moeilijker te lezen. En gedeelte zal gewoon gewenning zijn, maar was is nu het probleem wat wordt opgelost? Expliciet types opgeven lijkt mij een stuk minder foutgevoelig. En ik kan prima volgen dat er situaties zijn waar het prima is (eg zoals deze: Rickets in "[C#][discussie] Lekker veel var gebruiken?").

Maar gemiddeld genomen lijkt het me gewoon minder foutgevoelig als je expliciet types opgeeft, en errors/warnings krijgt als die niet kloppen. En ik vind het ook wel handig om direct te zien of een type signed of unsigned is, int8, 16, 32 of 64 is, of een float is. Al vermoed ik dat het dus ook ervan afhangt wat je doet, als je allemaal code hebt zoals het voorbeeld die in mijn link hierboven zit, dan snap ik dat var lekker werkt. Als je primair native data types gebruikt, dan vind ik het onhandig.

[supersnathan94]

Ik vind deze discussie wel grappig aangezien hij nu al meer dan tien jaar loopt en ik kom toch een aantal voorbeelden tegen waarvan ik denk: huh?

En dan heb ik het over dingen als:

code:

var ms = new MemoryStream();
var mat = new Mat<Vec4b>(h, w, buf);
var matBGR = new Mat<Vec3b>();
using var tif = Tiff.Open(sourceImagePath, "r");

List<String> bad = new ArrayList<String>();
var good = new ArrayList<String>();

In al deze gevallen heb ik heel veel moeite met het gebruik van var. Uit niets wordt namelijk duidelijk wat var is, niet uit de namen en niet uit de initialisaties. Wat iemand anders terecht al aanhaalde is het java voorbeeld echt kompleet niet hoe je het zou doen in de praktijk.
Daarnaast is de naamgeving dusdanig onduidelijk dat var het laatste concern is.

code:

var ms = new MemoryStream(); // En wat gaan we doen met die MemoryStream(); 
var mat = new Mat<Vec4b>(h, w, buf); // mega specifiek in init, maar superambigu in decl. Why?

List<String> bad = new ArrayList<String>(); // YES indeed should've been: List<String> bad = new ArrayList<>(); 

var good = new ArrayList<String>(); // What type is it going to use now? I can tell you that it is not the one you needed.

Var is leuk voor in loopconstructs, maar gebruik het alsjeblieft niet met het excuus dat het beter leest. Integendeel het maakt het voor nieuwe collega's veeeeeel moeilijker om te zien wat er gebeurt. Gebruik het op plekken waar uit context heel snel afgeleid kan worden wat het onderliggende type is (foreach var item in shoppingList bijvoorbeeld)

Voor de rest gewoon lekker strongly typed. Var is luiheid die je uiteindelijk van achteren bijt in extra tijd die je nodig hebt dingen uit te leggen of te herschrijven. Zoals in het voorbeeld van de ArrayList werkt het ook totaal niet goed met interfaces. Var gooit echt een aantal basis principes door de war en dat moet je dus voorzichtig benaderen.

[RayNbow]

Ankona schreef op woensdag 16 september 2020 @ 10:47:
[...]

Fijn, dat je dat bedoelt maar het issue is zo ook wel duidelijk. [...] anders zou ik een voorbeeld in elkaar moeten knutselen naar het probleem toe. Iets wat niets toevoegt. (En een stuk concrete code doorspitten om in een regel iets te herkennen wat je met een simpele beschrijving ook kunt duiden voegt ook weinig toe)

Nou, nee, een concreet voorbeeld zou juist helpen.

Eerder zei je dit:

Het eerste waar ik dan meteen aan denk is het gedrag van operators op numerieke types. Met name delen is bij integers anders dan bij floating point types.

Maar ik zie geen voorbeeld waarbij een expliciet uitgeschreven type je hier gaat helpen?

C#:

var result = f() / g();

versus

C#:

double result = f() / g();

Mochten de returntypes van f en g beide int zijn, dan is het weliswaar zo dat in het eerste stuk code result van het type int is (en niet double), maar in beide voorbeelden heeft er een integerdeling plaatsgevonden.

[supersnathan94]

hoe is dit ooit code die je serieus gaat opleveren?

code:

var result = f() / g();

var is hier niet het probleem. Wat doet f, wat doet g en wat gaan we doen met result?

Wat voor type result heeft is uiteindelijk ook wel van belang, maar eerst die andere dingen eens fiksen.

[RayNbow]

supersnathan94 schreef op woensdag 16 september 2020 @ 11:07:
Ik vind deze discussie wel grappig aangezien hij nu al meer dan tien jaar loopt en ik kom toch een aantal voorbeelden tegen waarvan ik denk: huh?

En dan heb ik het over dingen als:

code:

var ms = new MemoryStream();
var mat = new Mat<Vec4b>(h, w, buf);
var matBGR = new Mat<Vec3b>();
using var tif = Tiff.Open(sourceImagePath, "r");

List<String> bad = new ArrayList<String>();
var good = new ArrayList<String>();

In al deze gevallen heb ik heel veel moeite met het gebruik van var. Uit niets wordt namelijk duidelijk wat var is, niet uit de namen en niet uit de initialisaties.

In het geval van bijv. mat zie je toch aan de RHS dat het een Mat<Vec4b> is? Waarom zou ik dat ook aan de LHS moeten herhalen?

code:

var mat = new Mat<Vec4b>(h, w, buf); // mega specifiek in init, maar superambigu in decl. Why?

Hoezo ambigu? Het type van mat is Mat<Vec4b>.

Voor de rest gewoon lekker strongly typed.

var *is strongly-typed*.

[RayNbow]

supersnathan94 schreef op woensdag 16 september 2020 @ 11:18:
hoe is dit ooit code die je serieus gaat opleveren?

code:

var result = f() / g();

Als je de rest van de draad gelezen had, dan had je kunnen uitvogelen dat ik om een codevoorbeeld vroeg waarin het gebruik van var resulteerde in ongewenst gedrag. Zonder dat er voorbeelden worden gegeven moet ik maar gissen met kunstmatige, abstracte voorbeelden.

[CodeCaster]

supersnathan94 schreef op woensdag 16 september 2020 @ 11:07:
Integendeel het maakt het voor nieuwe collega's veeeeeel moeilijker om te zien wat er gebeurt. Gebruik het op plekken waar uit context heel snel afgeleid kan worden wat het onderliggende type is (foreach var item in shoppingList bijvoorbeeld)

Ik hoor dat argument vaak, maar heb het in al die jaren nooit relevant gevonden.

Waarom zou zo'n nieuwe developer beter z'n werk kunnen doen als er staat foreach (ShoppingListItem item in shoppingList)? Domein, context en daaropvolgende code duiden al aan wat het type inhoudt en wat je ermee kunt doen.

Voor de rest is er IntelliSense (of hoe het in je favoriete IDE ook heet): houd de muispijl op var, en de IDE toont je het type.

RayNbow schreef op woensdag 16 september 2020 @ 10:15:
Maar in welke situatie met var zal dit voorkomen? Dit zal alleen gebeuren als het resultaat ergens al een int was en je dus niet hebt omgezet naar een double.

In dit geval:

C#:

float f = f();
float g = g();

float h = f / g;

Als f() en g() een int retourneren, wordt er zonder expliciete declaratie (var) integer division toegepast. Het compileert dus vrolijk en levert onverwachte resultaten op, met een expliciete declaratie wordt dat stilletjes geconverteerd omdat een int altijd in een float past.

[ Voor 40% gewijzigd door CodeCaster op 16-09-2020 11:27 ]

[RobIII]

supersnathan94 schreef op woensdag 16 september 2020 @ 11:07:
In al deze gevallen heb ik heel veel moeite met het gebruik van var. Uit niets wordt namelijk duidelijk wat var is,

Ik haal uit je betoog veel meer dat je moeite hebt met de variabelenaam ("ms" bijvoorbeeld) dan dat je moeite hebt met var. En dat is terecht, maar daar ging 't voorbeeld niet over (en dus is er, voor 't voorbeeld, waarschijnlijk weinig aandacht besteed aan zinvolle namen omdat 't daar niet over ging).

C#:

var memstream = new MemoryStream();
MemoryStream memstream = new MemoryStream();

Geef mij die eerste maar hoor.

C#:

var custlookup = new Dictionary<long, CustomerI>();
Dictionary<long, CustomerI> custlookup = new Dictionary<long, CustomerI>();

Again: doe mij die eerste maar.

supersnathan94 schreef op woensdag 16 september 2020 @ 11:07:
Var is luiheid die je uiteindelijk van achteren bijt in extra tijd die je nodig hebt dingen uit te leggen of te herschrijven.

Noem eens een voorbeeld wanneer 't van achteren bijt

supersnathan94 schreef op woensdag 16 september 2020 @ 11:07:
Var gooit echt een aantal basis principes door de war en dat moet je dus voorzichtig benaderen.

Helemaal niet Var is gewoon een shorthand:

C#:

var cust = new Customer();

Is gewoon:

C#:

Customer cust = new Customer();

Voor de compiler. Het compiled beide naar exact dezelfde IL. Eigenlijk schrijf je gewoon:

C#:

hee_compiler_zoek_effe_het_type_uit_dat_kun_je_prima cust = new Customer();

[ Voor 40% gewijzigd door RobIII op 16-09-2020 11:31 ]

[Ankona]

RobIII schreef op woensdag 16 september 2020 @ 11:27:

C#:

var memstream = new MemoryStream();
MemoryStream memstream = new MemoryStream();

Geef mij die eerste maar hoor.

C#:

var custlookup = new Dictionary<long, CustomerI>();
Dictionary<long, CustomerI> custlookup = new Dictionary<long, CustomerI>();

Again: doe mij die eerste maar.

Dit zijn precies voorbeeld zoals Microsoft het gebruik van var ook adviseert. Is dan ook puur cosmetisch waar je voorkeur ligt. Ik kan ermee leven maar het voegt niets toe en kan inconsistent zijn richting andere declaraties.

C#:

var EenOfAnderVaagObject = _serviceXYZ.CreateIets(); 

Dit is dus een voorbeeld zoals Resharper het zou willen. (Microsoft niet, die schrijven dan expliciete declaratie voor)

[YakuzA]

RobIII schreef op woensdag 16 september 2020 @ 11:27:
[...]
Ik haal uit je betoog veel meer dat je moeite hebt met de variabelenaam ("ms" bijvoorbeeld) dan dat je moeite hebt met var. En dat is terecht, maar daar ging 't voorbeeld niet over (en dus is er, voor 't voorbeeld, waarschijnlijk weinig aandacht besteed aan zinvolle namen omdat 't daar niet over ging).

C#:

var custlookup = new Dictionary<long, CustomerI>();
Dictionary<long, CustomerI> custlookup = new Dictionary<long, CustomerI>();

Again: doe mij die eerste maar.

Var is af en toe een geschenk uit de hemel als je een project hebt waar mensen meerdere linebreaks in de declaratie gaan aanbrengen omdat die zo lang wordt idd:

C#:

ParameterResponse<EnumServiceResult, ParameterResponse<EnumOperationResult, BlaBlaIngewikkeldeDtoNaam>> result = xxxx

[ Voor 23% gewijzigd door YakuzA op 16-09-2020 11:37 ]

[RobIII]

Ankona schreef op woensdag 16 september 2020 @ 11:35:

Ik ben het wel met je eens bij een CreateIets() maar bij een GetCustomerById(123); verwacht ik toch écht een customer en vind ik var prima kunnen. In veruit de meeste gevallen (in ieder geval die ik tegen kom) is dat prima af te leiden / duidelijk en héél soms met een piepkleinbeetje domeinspecifieke kennis te bepalen. Ik kom, zo uit het hoofd althans, zelden gevallen tegen waar je echt een CreateSomething() hebt. En, helemaal eens, daar zou ik dan geen var gebruiken (of een var gebruiken en een cast ofzo).

YakuzA schreef op woensdag 16 september 2020 @ 11:36:

Exact; en nog een tandje erger:

C#:

ParameterResponse<EnumServiceResult, ParameterResponse<EnumOperationResult, BlaBlaIngewikkeldeDtoNaam>> foo = new ParameterResponse<EnumServiceResult, ParameterResponse<EnumOperationResult, BlaBlaIngewikkeldeDtoNaam>>(x, y, z);

Dan ben je IMHO echt wel een masochist als je daar geen var gebruikt.

[ Voor 25% gewijzigd door RobIII op 16-09-2020 11:52 ]

[farlane]

Ankona schreef op woensdag 16 september 2020 @ 11:35:
Dit zijn precies voorbeeld zoals Microsoft het gebruik van var ook adviseert. Is dan ook puur cosmetisch waar je voorkeur ligt. Ik kan ermee leven maar het voegt niets toe en kan inconsistent zijn richting andere declaraties.

var gebruiken in deze situaties voegt wat toe in de zin dat het het informatie duplicatie voorkomt, en dan is het wat mij betreft betere code.

In zijn boek houdt de heer Meyers een betoog waarom "auto" (de C++ variant van "var") 'a good thing' is. Ik vond het overtuigend in ieder geval.

[supersnathan94]

CodeCaster schreef op woensdag 16 september 2020 @ 11:21:
[...]
Waarom zou zo'n nieuwe developer beter z'n werk kunnen doen als er staat foreach (ShoppingListItem item in shoppingList)? Domein, context en daaropvolgende code duiden al aan wat het type inhoudt en wat je ermee kunt doen.

En in precies dat voorbeeld zeg ik ook dat het daar gewoon een prima manier is om te gebruiken. Daar kun je afspraken over maken intern die consistent te houden zijn.

Voor de rest is er IntelliSense (of hoe het in je favoriete IDE ook heet): houd de muispijl op var, en de IDE toont je het type.

[...]

In dit geval:

C#:

float f = f();
float g = g();

float h = f / g;

Als f() en g() een int retourneren, wordt er zonder expliciete declaratie (var) integer division toegepast. Het compileert dus vrolijk en levert onverwachte resultaten op, met een expliciete declaratie wordt dat stilletjes geconverteerd omdat een int altijd in een float past.

Dat is dus een van de voorbeelden waarin het gruwelijk fout zal gaan.

[farlane]

supersnathan94 schreef op woensdag 16 september 2020 @ 14:28:
Dat is dus een van de voorbeelden waarin het gruwelijk fout zal gaan.

Waarom gaat het daar fout?

[supersnathan94]

RobIII schreef op woensdag 16 september 2020 @ 11:27:
[...]

Ik haal uit je betoog veel meer dat je moeite hebt met de variabelenaam ("ms" bijvoorbeeld) dan dat je moeite hebt met var. En dat is terecht, maar daar ging 't voorbeeld niet over (en dus is er, voor 't voorbeeld, waarschijnlijk weinig aandacht besteed aan zinvolle namen omdat 't daar niet over ging).

En dat is dus precies waarom je dit soort dingen niet zou moeten gebruiken denk ik zelf. het dwingt je namelijk om na te denken over het type wat je wil hebben. ik weet niet in hoeverre C# het gebruik van interfaces heeft geregeld, maar daar ga je dan dus al direct de mist mee in. Het werkt inconsistentie in de hand, want interface types ga je hiermee dus nooit kunnen inferren.

Noem eens een voorbeeld wanneer 't van achteren bijt

code:

var cust = new MaleCustomer();

Gaat de compiler dan snappen dat je Customer als interface type wil gebruiken? Zo niet dan moet je dat weer expliciet maken en zo krijg je inconsistentie in hoe je variabelen declareert. Als je dit met zijn allen afspreekt (we gebruiken altijd var tenzij we een superType nodig hebben) dan heb ik daar verder geen problemen mee, maar dan moet je dat wel doen.

Eigenlijk schrijf je gewoon:

C#:

hee_compiler_zoek_effe_het_type_uit_dat_kun_je_prima cust = new Customer();

En dat kan ie dus niet altijd right?

[farlane]

supersnathan94 schreef op woensdag 16 september 2020 @ 14:37:
[...]

code:

var cust = new MaleCustomer();

Gaat de compiler dan snappen dat je Customer als interface type wil gebruiken?

Ja. Als jij die meegeeft aan een functie die een interface verwacht en je type voldoet daar aan dan kan dat.

En dat kan ie dus niet altijd right?

Ja dat kan wel : op plekken waar var gebruikt kan worden kan *altijd* het statische type worden geinferred.

Als je een ander type wilt dan de compiler vindt dat ie is moet je casten, maar net zo goed als in het C voorbeeld is een expliciete cast veel duidelijker dan een impliciete.

[ Voor 14% gewijzigd door farlane op 16-09-2020 14:44 ]

[supersnathan94]

farlane schreef op woensdag 16 september 2020 @ 14:30:
[...]

Waarom gaat het daar fout?

Omdat integer division. Als je daar dus niet expliciet een float declareert, je nooit decimalen gaat krijgen van 2 integers. integer division geeft je truncation. 1/2 is dus 0, -5/2 geeft je -2.

dit soort dingen wil je echt expliciet in je code hebben, want als er iets fout gaat (and it will) dan zie je dus niet 1,2,3 waarom.

farlane schreef op woensdag 16 september 2020 @ 14:41:
[...]

Ja. Als jij die meegeeft aan een functie die een interface verwacht en je type voldoet daar aan dan kan dat.


[...]

Ja dat kan wel : op plekken waar var gebruikt kan worden kan *altijd* het statische type worden geinferred.

Oke fair enough

Maar is dit ook slim vanuit onderhoudsperspectief?

again code schrijf je niet omdat je er nooit meer naar hoeft te kijken, als je hier afspraken over kan maken met je team sure go ahead, maar lijkt mij echt niet slim om dergelijke constructen zonder afspraken hierover zomaar in je codebase toe te passen.

Code moet namelijk meestal onderhouden worden door iemand anders dan jij. Zij moeten het dus ook snel kunnen snappen.

[farlane]

supersnathan94 schreef op woensdag 16 september 2020 @ 14:46:
Omdat integer division. Als je daar dus niet expliciet een float declareert, je nooit decimalen gaat krijgen van 2 integers. integer division geeft je truncation. 1/2 is dus 0, -5/2 geeft je -2.

Dat is alleen van belang als van f *en* g het return type wijzigt van float naar int, zodat de compiler plots een int division gaat doen ipv een float.

Als je dat return type wijzigt (van either functie) van float naar int moet je sowieso kijken naar je callers want er is kans op loss of information, aangezien in jouw situatie plots ints aan floats worden toegewezen, terwijl dat met var niet het geval is.

Het is wat mij betreft lood om oud ijzer.

Maar is dit ook slim vanuit onderhoudsperspectief?

Ja, het zorgt zelfs voor minder onderhoud denk ik.

[ Voor 7% gewijzigd door farlane op 16-09-2020 14:57 ]

[Ankona]

supersnathan94 schreef op woensdag 16 september 2020 @ 14:37:

[...]

code:

var cust = new MaleCustomer();

Gaat de compiler dan snappen dat je Customer als interface type wil gebruiken? Zo niet dan moet je dat weer expliciet maken en zo krijg je inconsistentie in hoe je variabelen declareert. Als je dit met zijn allen afspreekt (we gebruiken altijd var tenzij we een superType nodig hebben) dan heb ik daar verder geen problemen mee, maar dan moet je dat wel doen.

In theorie klopt dit, maar dit is niet iets waar je snel mee in de problemen komt. Zelf leg ik ook graag zoveel mogelijk dependencies op interfaces, maar dat speelt vooral bij DI.
Lokale variabelen ken je meestal maar een keer een waarde toe (anders is er misschien iets anders wat aandacht vraagt)

Om jouw code problematisch te maken:

code:

var cust = new MaleCustomer();

cust.DoeIets();

cust  = new FemaleCustomer(); // auw!

Waar dit gewoon zou werken: (Maar daarmee nog geen goede code is. )

code:

ICustomer cust = new MaleCustomer();

cust.DoeIets();

cust  = new FemaleCustomer();

[farlane]

Ankona schreef op woensdag 16 september 2020 @ 15:07:
Om jouw code problematisch te maken:

code:

var cust = new MaleCustomer();

cust.DoeIets();

cust  = new FemaleCustomer(); // auw!

Waarom is dat auw? Wat gebeurt daar volgens jou? Het kan nooit zo zijn dat in het tweede geval een FemaleCustomer voor een MaleCustomer wordt aangezien nl.

Of je code werkt (beide implementeren een base class/interface, maar dan moet je de eerste casten) of je compiler gaat klagen.

[ Voor 13% gewijzigd door farlane op 16-09-2020 15:12 ]

[Ankona]

farlane schreef op woensdag 16 september 2020 @ 15:10:
[...]

Waarom is dat auw? Wat gebeurt daar volgens jou? Het kan nooit zo zijn dat in het tweede geval een FemaleCustomer voor een MaleCustomer wordt aangezien nl.

Of je code werkt (beide implementeren een base class/interface, maar dan moet je de eerste casten) of je compiler gaat klagen.

Probeer maar, de compiler zal je een error tonen. De variabele heeft namelijk het type MaleCustomer gekregen, niet de interface of supertype.

[farlane]

Ankona schreef op woensdag 16 september 2020 @ 15:16:
[...]

Probeer maar, de compiler zal je een error tonen. De variabele heeft namelijk het type MaleCustomer gekregen, niet de interface of supertype.

Ja dat zeg ik. Dat is toch goed? Je doet iets waar de compiler het niet mee eens is. Op geen enkel moment zorgt "var" er voor dat er iets onverwachts gebeurt.

[Ankona]

farlane schreef op woensdag 16 september 2020 @ 15:19:
[...]


Ja dat zeg ik. Dat is toch goed? Je doet iets waar de compiler het niet mee eens is. Op geen enkel moment zorgt "var" er voor dat er iets onverwachts gebeurt.

Tja, niet werkende code is m.i. toch wel een auw. Dat je om toch var te gebruiken een work-around hebt middels casten maakt het niet mooier.

[ThomasG]

Ankona schreef op woensdag 16 september 2020 @ 15:16:
[...]

Probeer maar, de compiler zal je een error tonen. De variabele heeft namelijk het type MaleCustomer gekregen, niet de interface of supertype.

Dat is toch ook niet zo raar, maar gewoon wat je verwacht. new MaleCustomer kun je zien als een functie dat een MaleCustomer returned. Het zou raar zijn als dat ineens een ICustomer wordt. Als je dat wél wilt, moet je dat zelf aangeven. Maar dat heeft weinig met var te maken. Var gebruik je op plekken waar het overbodig is om het type in de declaratie te zetten, wat het in dat geval dus niet is.

[farlane]

Ankona schreef op woensdag 16 september 2020 @ 15:22:
[...]

Tja, niet werkende code is m.i. toch wel een auw. Dat je om toch var te gebruiken een work-around hebt middels casten maakt het niet mooier.

Niet werkende code moet gefixed worden, dat ben ik met je eens. Specifiek casten naar het supertype icm met var is wmb een heel duidelijk verhaal en geeft precies aan wat je wilt, terwijl de impliciete cast in jouw versie subtieler is, en eigenlijk onduidelijker (eye of beholder en zo)

C#:

    var cust = new MaleCustomer() as ICustomer;

    cust.DoeIets();

    cust  = new FemaleCustomer() as ICustomer;

    cust.DoeIets();

Of je gebruikt 2 aparte variabelen wat in dit stomme voorbeeld eigenlijk veel beter zou zijn

C#:

    var male = new MaleCustomer();

    male.DoeIets();

    var female  = new FemaleCustomer();

    female.DoeIets();

[ Voor 28% gewijzigd door farlane op 16-09-2020 15:51 ]

[KNed]

Heerlijk, de var discussie

Ik was ook tegenstander, maar inmiddels niet zo erg meer. Mits er goede duidelijke namen gebruikt worden.
Ik zie hier nu voorbeelden langs komen die met var gewoon lekkerder lezen.

De laatste posts tussen @farlane en @Ankona laten zien dat het maar net is wat je doel is.
Als je iets met de interface of supertype wil doen dan voldoet var niet.
Mijn stelling zou dan zijn:
-Gebruik je nooit die interface, doe dan lekker overal var.
-Gebruik je het door elkaar doe dan overal specifieke types voor ICustomer/MaleCustomer/FemaleCustomer om het verschil duidelijk te maken.

[Ankona]

farlane schreef op woensdag 16 september 2020 @ 15:46:
[...]


Niet werkende code moet gefixed worden, dat ben ik met je eens. Specifiek casten naar het supertype icm met var is wmb een heel duidelijk verhaal en geeft precies aan wat je wilt, terwijl de impliciete cast in jouw versie subtieler is, en eigenlijk onduidelijker (eye of beholder en zo)

C#:

    var cust = new MaleCustomer() as ICustomer;

    cust.DoeIets();

    cust  = new FemaleCustomer() as ICustomer;

    cust.DoeIets();

Of je gebruikt 2 aparte variabelen wat in dit stomme voorbeeld eigenlijk veel beter zou zijn

C#:

    var male = new MaleCustomer();

    male.DoeIets();

    var female  = new FemaleCustomer();

    female.DoeIets();

Je eerste fix (met as) doet eigenlijk nog iets anders. Die zet een null reference als de cast niet uitgevoerd kan worden.

Zonder twijfel is je tweede fix de enige juiste oplossing, maar daarmee is het voorbeeld ook gelijk weg. Wat ik aan het begin ook al aangaf, een nieuwe toekenning aan een bestaande variabele is zelden een goed idee en duidt vaak op te veel responsibilities. (Wat dan ook weer na de fix nog steeds het geval is maar dan krijg je een hele andere discussie.... ik kan mijn team ook dagen van het werk houden met dit soort zeer interessante en leerzame discussies..... wordt de klant alleen niet altijd even blij als we ons sprintdoel daardoor niet halen)

[RobIII]

Ankona schreef op woensdag 16 september 2020 @ 16:01:
[...]

Je eerste fix (met as) doet eigenlijk nog iets anders. Die zet een null reference als de cast niet uitgevoerd kan worden.

Dan doe je (ICustomer)MaleCustomer

Wat mensen niet (altijd) lijken te snappen is dat var niks anders is dan syntactic sugar; je compiler inferred het type (MaleCustomer) en maakt cust dus ook daadwerkelijk dat type; het "blijft" geen var. Als je er dus verderop een FemaleCustomer in probeert te stoppen gaat 't niet werken. Wél als je cast naar ICustomer (en beide types ICustomer implementeren uiteraard). Either way: Een var "bestaat niet"; je compiler maakt er meteen, daar, op dat moment het juiste (al dan niet expliciet gecaste) type van en vanaf daar is heel het "var" concept verleden tijd voor die variabele.

Ankona schreef op woensdag 16 september 2020 @ 16:01:
een nieuwe toekenning aan een bestaande variabele is zelden een goed idee

Daarom is dat (geforceerde) voorbeeld ook geen goed voorbeeld; het heeft niets te maken met nieuwe toekenningen maar met het voorkomen van:

C#:

EenDictionaryVanType<FooDinges, BarDinges> mijnvariabele = new HierMagIkNogEenKeerDatzelfdeStommeTypeHelemaalUitTypenWatIkNetOokAlHebGedaan<FooDinges, BarDinges>();

'

C#:

CustomerDictionary<CustomerKey, Customer> myCustomers1 = new CustomerDictionary<CustomerKey, Customer>();

//vs

var myCustomers2 = new CustomerDictionary<CustomerKey, Customer>();

Onder de streep zijn myCustomers1 en 2 exact hetzelfde type. De myCustomers variabele "blijft" geen var zodat je er een paar regels later een int aan kunt toewijzen. Daar heb je object voor (en dan heb je hele andere problemen ).

[ Voor 35% gewijzigd door RobIII op 16-09-2020 16:12 ]

[Woy]

Sowieso moet ik zeggen dat het in mijn code niet vaak voorkomt dat ik een lokale variabele assign, en dan bewust wil dat het gedeclareerde type een van de geimplemeteerde interfaces/superclasses is. Of het is een lokaal object waar het prima een concreet type mag zijn, of het komt al uit een factory method o.i.d. die al netjes als return type een interface heeft.

Daarmee is het ook een beetje een moot point, want in dat geval zal ik inderdaad terug vallen op een expliciete declaratie ( Wat in mijn geval een kleine voorkeur heeft boven het casten van de value )

[ Voor 9% gewijzigd door Woy op 16-09-2020 16:43 ]

[Haan]

Ik ben zelf ook voorstander van wél zoveel mogelijk var gebruiken. Bij mij in het bedrijf is dat ook de richtlijn. En natuurlijk zijn er gevallen waarin je soms wel het type expliciet wilt gebruiken en natuurlijk zijn er allerlei geforceerde voorbeelden waarin het misschien minder handig is, maar verder heeft var bijna alleen maar voordelen.
Alleen in onderstaande situatie kan var een beetje onhandig uitpakken, maar in principe kom je er dan ook wel weer snel genoeg achter dat je iets vergeten bent.

C#:

public async Task DoSomething()
{
    var input = await _someService.GetInputAsync(); 
    var foo = _someOtherService.GetFooAsync(input); // result is een Task ipv een Foo object
}

[pedorus]

offtopic:
Mooi om te zien dat de discussie nog niet is afgesloten

Ankona schreef op dinsdag 15 september 2020 @ 23:28:
Weet iemand de echte reden waarom Microsoft en zeker Resharper zulke fans zijn van var? Sommige teams leunen blind op deze aanbevelingen wat discussies erg lastig maakt.

Volgens mij maakt resharper daar geen geheim van:

quote: https://www.jetbrains.com...word_in_Declarations.html

it improves readability in many scenarios

Maar ze zijn flexibel, dus je kunt het configureren. Ik zit nog steeds in 'kamp var', dat leest het beste, maar een paar keer per jaar moet je toch een IDE opstarten om een type te achterhalen. Dat is een kleine prijs voor het veelal snellere leeswerk.

Ankona schreef op woensdag 16 september 2020 @ 15:07:

code:

var cust = new MaleCustomer();

cust.DoeIets();

cust  = new FemaleCustomer(); // auw!

In nieuwere talen (Scala, Kotlin, evt Go met const) heb je vaak ook een onderscheid tussen var en val. val (een niet opnieuw te assignen waarde) heeft vaak de voorkeur. In zo'n geval zou ik het als onhandig zien om de variabele te hergebruiken en 2 vals met andere namen gebruiken, maar het is deels een kwestie van smaak. Ik zou het dus zelf juist als voordeel zien dat dit niet kan.

[RobIII]

Haan schreef op woensdag 16 september 2020 @ 19:31:

Alleen in onderstaande situatie kan var een beetje onhandig uitpakken, maar in principe kom je er dan ook wel weer snel genoeg achter dat je iets vergeten bent.

C#:

public async Task DoSomething()
{
    var input = await _someService.GetInputAsync(); 
    var foo = _someOtherService.GetFooAsync(input); // result is een Task ipv een Foo object
}

In dat voorbeeld is de assignment naar foo sowieso nutteloos (en zou je een discard kunnen gebruiken) en zeurt VS iig over het niet awaiten van een async method (en over een unused var foo dus). Dus ook hier zie ik niet echt een probleem - of je moet blind zijn voor warnings (waar ik sowieso al jeuk van krijg, maar dat is een andere discussie ) of werken in notepad ofzo (als een holbewoner )

Gerelateerd en interessant leesvoer: https://ericlippert.com/2009/01/26/why-no-var-on-fields. Maar voordat je dat leest: onthou dat het in 2009 is geschreven, aan het eind staat een 2020 update.

[ Voor 12% gewijzigd door RobIII op 16-09-2020 19:55 ]

[Haan]

RobIII schreef op woensdag 16 september 2020 @ 19:49:

In dat voorbeeld is de assignment naar foo sowieso nutteloos (en zou je een discard kunnen gebruiken) en zeurt VS iig over het niet awaiten van een async method (en over een unused var foo dus). Dus ook hier zie ik niet echt een probleem - of je moet blind zijn voor warnings (waar ik sowieso al jeuk van krijg, maar dat is een andere discussie ) of werken in notepad ofzo (als een holbewoner )

Nee VS zeurt hier juist niet, omdat erboven wel een await staat

Overigens, om alle leesbaarheids-argumenten tegen var meteen van tafel te vegen, Resharper kan dit doen voor je :

[CodeCaster]

Haan schreef op donderdag 17 september 2020 @ 08:47:
[...]

Nee VS zeurt hier juist niet, omdat erboven wel een await staat

Overigens, om alle leesbaarheids-argumenten tegen var meteen van tafel te vegen, Resharper kan dit doen voor je : [Afbeelding]

Ja, maar dát is meteen de meest onzinnige feature ooit. Nou ja, misschien op de "inconsistent line endings" warning na. (edit: die is niet per se onzinnig, en van VS ipv R#) maar wel irritant als je je Git niet goed instelt)

De nieuwste Visual Studio heeft die hints ook gejat (ik ga m'n ReSharper ook niet meer verlengen, MS bouwt de nuttigste features toch wel in), ook voor functieparameters. Je code wordt friggin' onleesbaar met al die hints.

[ Voor 7% gewijzigd door CodeCaster op 17-09-2020 09:24 ]

[Ankona]

Ik ben eigenlijk ook totaal geen fan (meer) van Resharper. Visual Studio heeft bijna alle goeds overgenomen en werkt zonder Resharper soepeler en stabieler. (Die drukte in beeld met al die extra hints bevalt mij ook niet)

Enige wat lekker werkt is de ctrl-t zoek functie. Werk in mijn huidige project aan een spaghetti monoliet dus dan heb je dergelijke hulpmiddelen wel nodig.

[RobIII]

Haan schreef op donderdag 17 september 2020 @ 08:47:
[...]

Nee VS zeurt hier juist niet, omdat erboven wel een await staat

Ghe... is me nooit opgevallen
Dan nog loop je er vanzelf tegenaan omdat foo dan een Task<T> is i.p.v. een T die je daar verwacht (als je de await dus zou 'vergeten').

[ Voor 26% gewijzigd door RobIII op 17-09-2020 09:24 ]

[R4gnax]

Ankona schreef op woensdag 16 september 2020 @ 15:22:
[...]

Tja, niet werkende code is m.i. toch wel een auw. Dat je om toch var te gebruiken een work-around hebt middels casten maakt het niet mooier.

Ipv een workaround kun je ook gewoon kiezen om niet twee keer aan dezelfde lokale variable te assignen.

C#:

var male = new MaleCustomer();

male.DoeIets();

var female = new FemaleCustomer();

Wordt er nog beter leesbaar op, want je hoeft niet teruguit te scannen om te kijken wat er op dat ene moment ook al weer in die variable zat.

[EDIT]
Zie net dat @farlane dit ook al aanhaalde.
Ben dus niet de enige die ziet dat het gewoon een stom en geconstrueerd voorbeeld is. Daar heeft iemand gewoon een probleem bij een vooringenomen oplossing gezocht.

Dat is eigenlijk onderliggend aan de hele var discussie: van alle problemen 'met var' ligt het overgrote merendeel niet aan het gebruik van var, maar aan iets anders.

Ook het integer division voorbeeld ligt in die categorie. Want als je in bestaande software het return type van een bestaande public of protected method aanpast naar een nauwer type zonder naar usages te kijken, dan ben je eigenlijk per definitie al fout bezig.

[ Voor 35% gewijzigd door R4gnax op 22-09-2020 20:02 ]

[farlane]

R4gnax schreef op dinsdag 22 september 2020 @ 19:53:
[...]
Ook het integer division voorbeeld ligt in die categorie. Want als je in bestaande software het return type van een bestaande public of protected method aanpast naar een nauwer type zonder naar usages te kijken, dan ben je eigenlijk per definitie al fout bezig.

farlane in "[C#][discussie] Lekker veel var gebruiken?"