Het is alleen een echte hetze als het uit Hetzerath komt, anders is het gewoon sprankelende ophef.
En veruit de meeste mensen bloedgroep A?
Nee, O komt het meeste voor, daarna A, B en als laatste AB.
A is 42 procent van de bevolking (35 procent A+, 7 procent A-)
O is 46.5 procent van de bevolking (39.5 procent O-positief , 7 procent O- )
B is 8 procent van de bevolking (6,7 procent B+, 1,3 procent B-negatief)
AB is 3 procent van de bevolking (2,5 procent AB+, 0,5 procent AB-)
(die 0.5 procent die overblijft is afrondings-verschil)
Zie https://www.sanquin.nl/do...elke-bloedgroepen-zijn-er
[ Voor 8% gewijzigd door wildhagen op 19-03-2020 09:07 ]
Virussen? Scan ze hier!
Daarvoor is uiteraard gecompenseerd.Hsb-3 schreef op donderdag 19 maart 2020 @ 08:56:
Of zouden er minder mensen met bloedgroep 0 zware symptomen hebben omdat er minder mensen zijn met 0?
En veruit de meeste mensen bloedgroep A?
Stel dat 50% van de bevolking bloedgroep A heeft en 10% bloedgroep 0, maar onder de patiënten vind je 60% met bloedgroep A en 5% met bloedgroep 0, dan is dat best een significant verschil. Cijfers staan ook gewoon in het pers-artikel en in het wetenschappelijke artikel.
@wildhagen dan heb ik dus met 0+ de meestvoorkomende bloedgroep.
[ Voor 6% gewijzigd door Mx. Alba op 19-03-2020 09:07 ]
Het is alleen een echte hetze als het uit Hetzerath komt, anders is het gewoon sprankelende ophef.
*Update: domme vraag sorry.
Wereldwijd dus ook grootste aandeel bloedgroep o
https://mens-en-gezondhei...st-of-het-minst-voor.html
Ook interessant om dan te lezen hoe dit bericht geïnterpreteerd moet worden:
https://www.gezondheidenw...-a-vatbaarder-voor-corona
[ Voor 96% gewijzigd door Stevie_ op 19-03-2020 09:33 ]
Nou is alleen de vraag nog: zijn deze percentages hetzelfde voor China c.q. alle bevolkingsgroepen over de hele wereld. Ik zou me kunnen voorstellen dat de verhoudingen anders liggen bij Aziatische mensen dan bij mensen van een Caucasische afkomst...wildhagen schreef op donderdag 19 maart 2020 @ 09:02:
[...]
Nee, O komt het meeste voor, daarna A, B en als laatste AB.
A is 42 procent van de bevolking (35 procent A+, 7 procent A-)
O is 46.5 procent van de bevolking (39.5 procent O-positief , 7 procent O- )
B is 8 procent van de bevolking (6,7 procent B+, 1,3 procent B-negatief)
AB is 3 procent van de bevolking (2,5 procent AB+, 0,5 procent AB-)
(die 0.5 procent die overblijft is afrondings-verschil)
Zie https://www.sanquin.nl/do...elke-bloedgroepen-zijn-er
Hier kan je het per land zien: Wikipedia: Blood type distribution by countryservies schreef op donderdag 19 maart 2020 @ 10:10:
[...]
Nou is alleen de vraag nog: zijn deze percentages hetzelfde voor China c.q. alle bevolkingsgroepen over de hele wereld. Ik zou me kunnen voorstellen dat de verhoudingen anders liggen bij Aziatische mensen dan bij mensen van een Caucasische afkomst...
In China is O dus ongeveer net zo veel als in Nederland (iets minder dan de helft van de bevolking), maar A een stuk minder (27 procent tegen 42 procent in NL). China zit vooral met B+ hoger dan NL (bijna 19 procent van de bevolking, tegen 6.7 procent in NL)
Grappig dat voor NL daar overigens weer andere wearden staan dan Sanquin, de officiele bloedbank, aangeeft....
[ Voor 7% gewijzigd door wildhagen op 19-03-2020 10:16 ]
Virussen? Scan ze hier!
Maar het is zeker de moeite waard om die associatie tzt met een onderzoek uit te zoeken waarbij het beter mogelijk is voor confounders etc te controleren.
[ Voor 4% gewijzigd door begintmeta op 19-03-2020 13:43 ]
[ Voor 55% gewijzigd door begintmeta op 19-03-2020 11:56 ]
Verwijderd
[ Voor 67% gewijzigd door Standeman op 19-03-2020 13:45 ]
In ieder geval is het onderzoek niet robuust genoeg om iets meer te zijn dan een aanleiding voor verder onderzoek zou ik zeggen.Verwijderd schreef op donderdag 19 maart 2020 @ 13:15:
Dit soort uitspraken zonder enige onderbouwing voegen niets toe
[ Voor 12% gewijzigd door Standeman op 19-03-2020 13:46 ]
Die staan gewoon in het artikel. Ik vind trouwens dat als mensen hier reageren ze op zijn minst het artikel moeten lezen, of heb ik toevallig er vanuit mijn werk toegang tot?servies schreef op donderdag 19 maart 2020 @ 10:10:
[...]
Nou is alleen de vraag nog: zijn deze percentages hetzelfde voor China c.q. alle bevolkingsgroepen over de hele wereld. Ik zou me kunnen voorstellen dat de verhoudingen anders liggen bij Aziatische mensen dan bij mensen van een Caucasische afkomst...
Het is gemeten, hoezo broodje aap? kun je dat uitleggen? Heb je het artikel gelezen?Verwijderd schreef op donderdag 19 maart 2020 @ 13:15:
Dit soort uitspraken zonder enige onderbouwing voegen niets toe
[ Voor 20% gewijzigd door Standeman op 19-03-2020 13:46 ]
Het is alleen een echte hetze als het uit Hetzerath komt, anders is het gewoon sprankelende ophef.
Dat is lastig te zeggen. Hoe wil je die mensen extra in bescherming nemen? Laat je anderen hun werk doen? Lopen die anderen dan misschien onnodig meer gevaar (misschien hebben anderen wel een andere, nog onbekende en misschien ook werkelijker, met covid-19 geassocieerde eigenschap). Geef je mensen met bepaalde bloedgroepen extra beschermende middelen? Heb je dan geen kans dat die anders nuttiger hadden kunnen worden gebruikt (dus onnodige schade)? Zou onderzoeksenergie en tijd beter hierin of in iets anders kunnen worden gestoken?Mx. Alba schreef op donderdag 19 maart 2020 @ 13:28:
...Wat voor schade doet het om uit voorzorg mensen met bloedgroep A wat extra in bescherming te nemen?...
Ik heb uiteraard eerst gelezen voordat ik heb gepost. www.medrxiv.org is in principe voor iedereen open.bvbal79 schreef op donderdag 19 maart 2020 @ 13:22:
[...]
Die staan gewoon in het artikel. Ik vind trouwens dat als mensen hier reageren ze op zijn minst het artikel moeten lezen, of heb ik toevallig er vanuit mijn werk toegang tot?
Sorry <knip>, maar wat ik vroeg heb ik niet terug kunnen vinden in het artikel, zowel niet in het kranten artikel als het wetenschappelijke...bvbal79 schreef op donderdag 19 maart 2020 @ 13:22:
[...]
Die staan gewoon in het artikel. Ik vind trouwens dat als mensen hier reageren ze op zijn minst het artikel moeten lezen, of heb ik toevallig er vanuit mijn werk toegang tot?
Ze hebben het tot nu toe ook alleen maar in China (Wuhan) kunnen testen. Op het ogenblik dat je het ergens anders test en dezelfde verhoudingen komen naar boven, dan kun je gaan veronderstellen dat de bloedgroep van invloed is en niet iets anders wat toevallig deze scheve verhouding veroorzaakt.
Klinkt beduidend vriendelijker dan met het weggeknipte...
[ Voor 5% gewijzigd door Ramzzz op 19-03-2020 18:05 ]
Het zou eventueel kunnen helpen bij overvolle ICU opnames en beademingen. Als iemand met type O meer kans heeft om te overleven omdat ze minder zware symptomen ontwikkelen zou je deze groep een minder hoge prioriteit kunnen geven.
Aan de andere kant: Misschien moet je dan O- juist de hoogste prioriteit geven omdat ze universele bloeddonoren (kunnen) zijn.
Moeilijke keuzes moeten toch gemaakt worden. Dit kan ook een rol gaan spelen.
- Dit hoort niet thuis op tweakers edit: blijkbaar is er een themaforum, niet gezien excuus
- Kap met dit soort speculatie! Hier wordt niemand beter van. Als dit soort dingen daadwerkelijk waar blijken te zijn hoor je er vanzelf wel van via betrouwbare bronnen.
[ Voor 10% gewijzigd door roger128 op 19-03-2020 16:50 ]
Ik begrijp het sentiment. Op zich eens dat speculatie niet echt zin heeft.roger128 schreef op donderdag 19 maart 2020 @ 16:50:Waarom bestaat dit topic?
- Dit hoort niet thuis op tweakers edit: blijkbaar is er een themaforum, niet gezien excuus
- Kap met dit soort speculatie! Hier wordt niemand beter van. Als dit soort dingen daadwerkelijk waar blijken te zijn hoor je er vanzelf wel van via betrouwbare bronnen.
Maar het heeft wel enige discussiewaarde - zij het totaal theoretisch en zonder dat we er enige waarde aan hoeven te hechten - en dit is Themaforum: Coronavirus.
We kijken het wel even aan.
"Atheism is an attitude, a frame of mind that looks at the world objectively, fearlessly, always trying to understand all things as a part of nature" - Carl Sagan
404 Signature not found
Hoezo weet de gemiddelde Nederlander dat niet?SMSfreakie schreef op donderdag 19 maart 2020 @ 17:18:
en hoe weet de gemiddelde nederlander nou welke bloedgroep die zo 1/2/3 heeft?
Hoe weet jij dat meer mensen het niet, dan wel weten?
Niet, tenzij je bijv. bloed doneert (maar ook dan hoef *jij* het niet per se te weten) of om wat voor reden een bloedtest hebt ondergaan (evt als onderdeel van iets). Als iemand het weet is het waarschijnlijk je huisarts, maar ik kan me zeer goed voorstellen dat die niet zit te wachten op duizenden belletjes van bezorgde mensen die nutteloze informatie willen weten. Je hebt er verder ook niks aan, veel meer dan "oh, statistisch gezien heb ik, als ik het virus krijg, kans op heftigere/mildere symptomen als ik dit artikel moet geloven". Het is niet alsof je je bloedgroep kan veranderen of er iets anders aan kan doen behalve de huidige maatregelen die je zonder kennis over dit al nam.SMSfreakie schreef op donderdag 19 maart 2020 @ 17:18:
en hoe weet de gemiddelde nederlander nou welke bloedgroep die zo 1/2/3 heeft?
Je kan zo'n papieren zelftest scoren voor een paar tientjes, maar hoe betrouwbaar die zijn valt nog te bezien.
Eventueel kan dit voor de wetenschap iets zijn waarmee ze meer kennis over het virus en/of de mogelijke bestrijding krijgen maar that's it for now.
Het schijnt dat ongeveer de helft het niet weet, hoewel ik daar zo gauw geen heel goede bron bij heb. Ik kan het me wel heel goed voorstellen, aangezien ik het ook niet weet, er van mij uit nooit een noodzaak is geweest om het zelf te weten en omdat ik me gewoon geen scenario kan voorstellen waarbij het voor jou zelf nuttige informatie is. Ook al weet je het, word je volgens mij altijd nog getest als het nog niet in je dossier staat. Er zijn gewoon veel te veel mensen die het verkeerd onthouden of gewoon maar wat roepen, en dat kan natuurlijk dodelijke gevolgen hebben.JdM schreef op donderdag 19 maart 2020 @ 17:33:
[...]
Hoezo weet de gemiddelde Nederlander dat niet?
Hoe weet jij dat meer mensen het niet, dan wel weten?
[ Voor 31% gewijzigd door DataGhost op 19-03-2020 17:42 ]
Dat kun je laten testen. Bijvoorbeeld als je bloeddonor wordt bij Sanquin, wordt (uiteraard) je bloedgroep bepaald.SMSfreakie schreef op donderdag 19 maart 2020 @ 17:18:
en hoe weet de gemiddelde nederlander nou welke bloedgroep die zo 1/2/3 heeft?
En misschien staat het al in je dossier bij de huisarts, als je al eens een bloedtest hebt gehad in het verleden, anders kun je hem er alsnog om vragen.
Ik heb iig A-positief
Virussen? Scan ze hier!
Verwijderd
Mag dat paniekzaaien en zogenaamd medisch advies dan verwijderd worden uit de ts? Dat is echt niet op zijn plaats.Ramzzz schreef op donderdag 19 maart 2020 @ 17:17:
[...]
Ik begrijp het sentiment. Op zich eens dat speculatie niet echt zin heeft.
Maar het heeft wel enige discussiewaarde - zij het totaal theoretisch en zonder dat we er enige waarde aan hoeven te hechten - en dit is Themaforum: Coronavirus.
We kijken het wel even aan.
Ik heb mijn kaart nog van de dienstkeuring met daarop de bloedgroepSMSfreakie schreef op donderdag 19 maart 2020 @ 17:18:
en hoe weet de gemiddelde nederlander nou welke bloedgroep die zo 1/2/3 heeft?
For it is the doom of men that they forget... Huidige en vroegere hardware specs The Z80 is still alive!
Laat ik 't omdraaien: waarom zouden mensen zich met een andere bloedgroep veiliger moeten wanen? Waarom alleen A "extra" beschermen? Want hoe ziet dan het slechtste geval er uit?Mx. Alba schreef op donderdag 19 maart 2020 @ 13:28:
Wat voor schade doet het om uit voorzorg mensen met bloedgroep A wat extra in bescherming te nemen? In het slechtste geval heb je dan onnodig mensen extra beschermd en dat is nog steeds positief, toch?
We moeten gewoon allemaal oppassen / ons best doen. Al helemaal omdat je zélf ook al zegt dat hoewel het onderzoek dan misschien wel wetenschappelijk onderbouwd is maar ook nog "in het stadium 'hee, dit is interessant, daar zouden we verder onderzoek naar moeten doen'" is. Laten we dan vooral geen conclusies gaan trekken en gewoon -allemaal- ons best doen 't niet verder te verspreiden en -iedereen- proberen (even goed) in bescherming te nemen.
[ Voor 3% gewijzigd door RobIII op 19-03-2020 17:54 ]
There are only two hard problems in distributed systems: 2. Exactly-once delivery 1. Guaranteed order of messages 2. Exactly-once delivery.
Je eigen tweaker.me redirect
Over mij
Ik weet in ieder geval dat ik O heb (geen idee of het O+ of O- is) omdat m'n beide ouders O hebben.SMSfreakie schreef op donderdag 19 maart 2020 @ 17:18:
en hoe weet de gemiddelde nederlander nou welke bloedgroep die zo 1/2/3 heeft?
Ipsa Scientia Potestas Est
NNID: ShinNoNoir
IMHO is die nu eigenlijk wel een beetje uitgeput.Ramzzz schreef op donderdag 19 maart 2020 @ 17:17:
... Maar het heeft wel enige discussiewaarde - zij het totaal theoretisch en zonder dat we er enige waarde aan hoeven te hechten ...
[ Voor 12% gewijzigd door begintmeta op 19-03-2020 18:03 ]
Tip, volgende keer dat je voor wat dan ook moet bloedprikken even vragen of ze ook je bloedgroep mee kunnen testen. Is voor zover ik weet nooit een probleem (hoewel het nu misschien n beetje overbelast is), zo heb ik de mijne ook gekregen.SMSfreakie schreef op donderdag 19 maart 2020 @ 17:18:
en hoe weet de gemiddelde nederlander nou welke bloedgroep die zo 1/2/3 heeft?
Paniekzaaien vind ik een beetje heel erg overdreven...Verwijderd schreef op donderdag 19 maart 2020 @ 17:38:
[...]
Mag dat paniekzaaien en zogenaamd medisch advies dan verwijderd worden uit de ts? Dat is echt niet op zijn plaats.
Om nou te zeggen dat je hier beschermingsmaatregelen op zou kunnen aanpassen lijkt me sterk. Daarvoor lijken mij de procentuele afwijkingen te klein te zijn.
Wat je misschien wel kunt afvragen is waarom zijn die verschillen er?(als ze er zijn) Wat is een verder verschil bij mensen met verschillende bloedgroepen. Wat versterkt de weerstand bij die ene bloedgroep? Dat ontdekken zou een goede hulp kunnen zijn bij de bestrijding van het virus...
[ Voor 1% gewijzigd door servies op 19-03-2020 21:26 . Reden: Iets duidelijker wat ik bedoelde ]
Dat kunnen we ons zeker afvragen, maar voorlopig moeten we ons ook nog steeds afvragen of die verschillen er ook echt zijn.servies schreef op donderdag 19 maart 2020 @ 19:02:
...
Wat je misschien wel kunt afvragen is waarom zijn die verschillen er? ...
Dit is natuurlijk grote onzin, ook de bloedgroepen hebben niks met de ernst van de aandoening te maken. Oftewel “correlation does not imply causation“
[ Voor 8% gewijzigd door gielie op 19-03-2020 20:31 ]
"Death smiles at us all, all a man can do is smile back." - Maximus Decimus Meridius
Belangrijke begrippen
Omdat dit soort data mogelijk wat rumoer met zich meebrengt zoals ook op te maken in de reacties, laat ik mijn respons op dit artikel hier geven.Allereerst belangrijk om al aan te geven, dit artikel is zoals aangegeven nog niet peer-reviewed, wees dan ook zeker als leek bedachtzaam op de inhoud.
Voor wat betreft de statistiek die in dit artikel naar voren komt is het belangrijk om kennis te nemen van een aantal begrippen:
Het relatieve risico (relative risk / risk ratio): De ratio van het risico op de uitkomst in één groep ten opzichte van het risico in een andere groep.
De odds ratio: De ratio van de odds in één groep ten opzichte van de odds in een andere groep.
Odds: De ratio van de uitkomst tegen de afwezigheid van de uitkomst.
Nog te volgen? Vermoedelijk lastig. Maar we gaan verder. Bij een risico van 1 op 4 (25%), dan zijn de odds (kans) 1 tegen 3 (33%). Nu wordt het vermoedelijk weer iets inzichtelijker, kans! Is het risico nu kleiner, bijv. 1 op 100 (1%), dan is de odds 1 tegen 99 (1.01%).
Wat doet dit er toe? Let op het verschil in percentage. Bij een groter risico, zijn de odds een minder valide afspiegeling van het risico. Met als gevolg, bij een groter voorkomen van een bepaalde factor binnen een groep, is een odds ratio mogelijk niet langer de beste methode om je data te presenteren, het kan een vertekening van de werkelijkheid geven.
Wat betekent dat voor dit artikel?
Berekenen we de data na, dan kun je dit verschil zelf zien: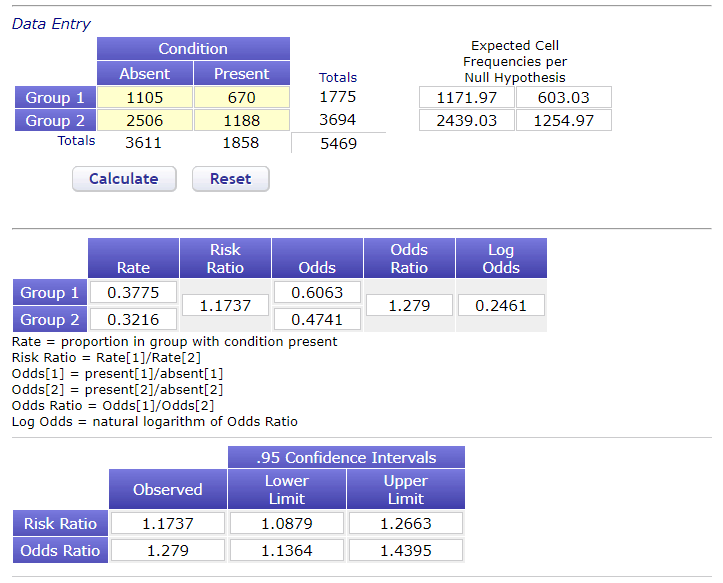
Mocht je willen, dan kun je de berekening zelf stapsgewijs meelopen op bijv. de volgende website:
http://vassarstats.net/odds2x2.html
Wat is hier gaande? Kijk naar Tabel 1 in het artikel. Daar zien we voor bloedgroep A bijv. de volgende data:
In de Wuhan populatie 670 patiënten met bloedgroep A, dit is in te vullen als "condition present" in één van de twee groepen. In de andere groep kun je de controle data invullen, 1188 met "condition" present. Maar wat is condition absent? Dit zijn de overige patiënten. De som van bloedgroep B, AB en O. Voor de controle groep zijn dit 2506 mensen, voor de Wuhan COVID-19 groep zijn dit 1105 mensen.
Druk je op calculate, dan zie je conform het manuscript een Odds ratio van 1.279, en een confidence interval van 1.136 - 1.4395 (1.440 afgerond).
Maar, wat je ook kunt zien is het relatieve risico (risk ratio) van 1.174 (1.088 - 1.2663). Hoewel dit een op het eerste oog klein verschil lijkt te zijn, tenslotte, we spreken maar over een verschil van ongeveer 0.1, is dit een verschil binnen een ratio. Met een odds ratio van 1.28 zou je kunnen stellen dat patiënten met bloedgroep A 28% meer likely zijn op COVID-19, maar met een relatief risico van 1.17 reduceren wij dit al naar 17%. Scheelt toch al weer 11%.
Dan komt de confidence interval om de hoek kijken. Dit vertelt ons iets over hoe zeker zijn wij over die 17%? In principe, niet. Vandaar het confidence interval, of in Nederlands betrouwbaarheidsinterval. De onder- en bovengrens hierbij geeft de grens aan van waar de daadwerkelijke waarde tussen zal liggen. Dit is in dit geval op basis van deze Wuhan data dus tussen de 1.09 en 1.27. Met andere woorden, een verhoogde kans tussen de 9 en 27% om een COVID-19 besmetting op te lopen met bloedgroep A.
Een optimist zou zeggen, doe mij die 9%, een pessimist zal zeggen het is die 27%. Maar voor beiden, laten we wel wezen, je hebt het hier dus niet eens over een verdubbeling van de kans, dat zou namelijk 100% zijn, oftewel een relatief risico van 2. Het is dus maar een kleine factor op individuele basis.
Qua mortaliteit, dan ziet het relatieve risico eruit als volgt: 1.28 (1.08 - 1.52), dit versus de odds ratio van 1.48 (1.11 - 1.97) zoals gerapporteerd binnen het manuscript. Ook in dit geval is een presentatie van het relatieve risico netter, en wederom dus lager en een relatief kleine kans.
De waarde van P-waarde
Daar komt bij, nu we het over kans hebben, de p-waarde. P van probability. Hoe moet je dit interpreteren? Een P-waarde van 0.05 wordt vaak gehanteerd binnen de medische literatuur als zijnde statistisch significant, maar wat betekent dit nu eigenlijk? Zo eenvoudig mogelijk gezegd houdt dit in dat er een kans is van 5% dat de getoetste nulhypothese (in dit geval de hypothese dat er geen associatie zou bestaan tussen bloedgroep A en COVID-19), juist is.Een significante uitslag met een P-waarde van 0.05 houdt dus in dat de kans 5% is dat deze uitslag onwaar is, puur op toeval gebaseerd. Een P-waarde van 0.008 maakt deze kans 0.8%. Binnen de medische literatuur accepteren wij dit veelal als sterk genoeg bewijs, maar blijft altijd iets om je bewust van te zijn. Zeker indien iets hoge implicaties heeft.
Blik op de meta-analyse
Ik hoop dat ik jullie aandacht nog heb! Maar ik kan begrijpen dat dit lastig kan zijn.In de meta analyse van de odds ratios zien we voor wat betreft de associatie tussen bloedgroep A en COVID-19 in figuur 1 het volgende:
OR 1.28 (1.14 - 1.44) voor de al beschreven populatie, met daarnaast een OR van 1.40 (0.95 - 2.05) en 1.00 (0.77 - 1.29) voor de andere twee populaties. Bovendien zie je een mooie overall met OR van 1.21 (1.02 - 1.43).
Wat gebeurd hier?
De Odds ratios van nummer 2 en 3 zijn verkregen op vergelijkbare wijze als nummer 1. Hierbij dus wederom de kanttekening dat het relatieve risico voor de Wuhan university data ook hier lager ligt dan de odds ratio's, namelijk RR 1.24 (0.98 - 1.56), voor de Shenzhen data blijft dit soortgelijk, RR 1.00 (0.83 - 1.20).
Omdat we in 2 populaties dus al een lager uitvallende RR dan OR hebben, is het netter om ook in de meta-analyse het relatieve risico te gebruiken.
Daarmee kom je binnen de meta-analyse dan per definitie ook uit op een overall RR lager dan OR, lager dan 1.21. Omdat dit wat meer werk is, ga ik deze data voor nu niet herbereken. Maar dus lager dan 21% verhoogd risico, maar let ook vooral op de betrouwbaarheids interval. Een potentiële kansverhoging van slechts 2%. Het potentiële relatieve risicoverhoging ligt mogelijk dus daarbij nog lager zelfs.
En let ook op de p-waarde voor deze OR, een P-waarde van 0.027. Oftewel, er is een 2.7% kans dat deze uitslag onwaar is op basis van puur toeval. Tegenover een mogelijk minimaal 2% potentiële kansverhoging op COVID-19 besmetting als bloedgroep type A. De optimist die in gaat zetten op kans weet het natuurlijk wel, de individuele kans om deze risicoverhoging af te schieten is daarmee mogelijk groter dan de verhoogde kans om COVID-19 te krijgen ;-).
Concluderend
Op basis van de data gepresenteerd in dit artikel ben ik dan ook helemaal niet zo overtuigd van het belang van bloedgroep A op COVID-19 susceptibiliteit. Het zou voorbarig zijn om te concluderen dat er hier een duidelijke associatie lijkt te bestaan.De volgende conclusie van de auteurs:
Vind ik zoals aldaar dan ook beschreven veel te stellig. Indien ik dit artikel ter review aangeboden zou krijgen zou ik deze conclusie op basis van de gegeven data dan ook retour sturen om te laten reviseren door de auteurs.This study may have potential clinical implications given the current COVID-19 crisis: (1) People with blood group A might need particularly strengthened personal protection to reduce the chance of infection; (2) SARS-CoV-2-infected patients with blood group A might need to receive more vigilant surveillance and aggressive treatment; (3) It might be helpful to introduce ABO blood typing in both patients and medical personal as a routine part of the management of SARS-CoV-2 and other coronavirus infections, to help define the management options and assess risk exposure levels of people.
Waar ik wel meer overtuiging in zie is de beschreven andere kant van de medaille, de beschreven verlaagde susceptibiliteit bij bloedgroep O. Maar ook hier telt wederom, relatieve risico! En dit is 0.76 (0.70 - 0.84) vs OR 0.68 (0.60 - 0.77), en daarmee toch ook al weer een stukje kleiner 'waar' verschil. Maar belangrijker, de meta-analyse toont hierin een meer overtuigend beeld. Hoewel zeker nog altijd te pleiten om dit nader te onderzoeken.
Juist in deze tijden is het belangrijk dat we niet gehaaste conclusies trekken en gepresenteerde data reviewen.
Hartelijk dank voor je heldere stuk.
Top!
[ Voor 4% gewijzigd door Mastermind op 19-03-2020 21:51 ]
Tenzij 1 van jouw ouders niet jouw ouder blijkt te zijn. Je moet toch echt zelf laten testen. Misschien had de melkboer wel bloedgroep A.RayNbow schreef op donderdag 19 maart 2020 @ 17:58:
[...]
Ik weet in ieder geval dat ik O heb (geen idee of het O+ of O- is) omdat m'n beide ouders O hebben.
Het is alleen een echte hetze als het uit Hetzerath komt, anders is het gewoon sprankelende ophef.
Of het zinvol is het bij een case-control-inderzoek over risks te hebben in plaats van odds is ook altijd maar de vraag.
| covid-19 | niet-covid-19 | |
| bloedgroep A | a | b |
| niet-bloedgroep-a | c | d |
Het risico op covid-19 in de bloedgroep-A-groep is a/(a+b), het risico op covid-19 in de niet-bloedgroep-A-groep is c/(c+d), het relatieve risico is (a/(a+b))/(c/(c+d)). b en d zijn in dit geval echter getallen die worden bepaald door de onderzoeker bij het sampelen van controls. Stel dat de onderzoekers 2x zo veel controls sampelen, wordt het (a/(a+2b))/(c/(c+2d)), dit zal het relatieve risico veranderen. De odds ratio blijft dan echter ongewijzigd, aangezien (a/b)/(c/d) gelijk aan (a/2b)/(c/2d) is. Voor het onderzoek naar associaties is een odds rato verder ook een prima uitkomstmaat zou ik zeggen. (op bijvoorbeeld deze pagina wordt het allemaal ook nog eens beschreven)
Ik zou dat toch anders interpreteren. Wat je hier uitrekent is de odds-ratio voor het hebben van bloedgroep A in de Wuhan Jinyintan Hospital-groep versus de Wuhan Area-groep. (odds bloedgroep A in area=1188/2506, odds bloedgroep A in hostpital=670/1105, odds ratio ((1188/2506)/(670/1105)=~1.28)psychodude schreef op donderdag 19 maart 2020 @ 21:07:
... Met een odds ratio van 1.28 ... meer likely zijn op COVID-19 ...
Over hoe het met de odds-ratio tussen covid-19 en bloedgroep zit zegt dat niet noodzaklijk veel. Zoals het is, is het eigenlijk een analyse van het voorkomen van bloedgroep A in twee groepen (je ziet ook uiteraard dat de 'rates' exact overeenkomen met de proportie van bloedgroep A in de betreffende groepen: 37,75% en 32,16%, en risk ratio is dan de quotiënt daarvan).
Je kruistabel heeft aan een kant [bloedgroep-A&niet-bloedgroep A], aan de andere kant [Wuhan Hospital&Wuhan Area]. Wat je zou willen is een kruistabel zoals die boven aan deze post, met aan een kant [bloedgroep-A&niet-bloedgroep A] en aan de andere kant [covid-19&niet-covid-19]. [Wuhan Hospital&Wuhan Area] is niet hetzelfde als [covid-19&niet-covid-19], tenzij het zo zou zijn dat de proporties van de bloedgroepen in de niet-covid-19-groep inderdaad overeenstemmen met de Wuhan Area-groep. Dat zou dan ook de verdeling van bloedgroepen zijn die je in de case-groep zou verwachten als bloedgroep geen associatie zou hebben.
Voor dit onderzoek naar covid-19 is nu min of meer gesteld dat de Wuhan Area-groep gelijk aan niet-covid-19 is, en de Wuhan Jinyintan Hospital-groep aan wel covid-19. Dat klopt natuurlijk ook (maar ook weer niet zie hieronder). Maar is dit wel een zinvolle vergelijking?
De covid-19-gevallen, de gevallen uit het ziekenhuis, zijn op zich prima. Het lastige punt is dat in een case-controle-onderzoek goed bij de cases passende controls geselecteerd moeten worden, of de steekproef uit 2015 daaraan voldoet, is in mijn ogen onvoldoende duidelijk. Dus is het inderdaad zo dat je, bij geen invloed van bloedgroep op de kans om covid-19 te hebben, een verdeling van bloedgroepen in de cases/Wuhan Hospital-groep overeenkomstig die in de controls/Wuhan Area-groep mogen verwachten?
Het valt op dat een onderzoek naar bloedgroepen van gezonde Han-Chinezen in Wuhan (tenminste dat zegt de titel) wordt gebruikt als referentiepopulatie (ik heb het originele artikel [Xu P, et al. Distribution of ABO and RhD blood group among Healthy Han population in Wuhan. J Clin Hematol (China). 2015(28):837] helaas zo 123 niet kunnen achterhalen). Nu zullen de Han-Chinezen in Wuhan ongetwijfeld de grootste ethnische groep zijn (zou best >90% of meer kunnen zijn), maar aangezien er ethnische verschillen qua bloedgroep binnen Wuhan zouden kunnen bestaan, zou het in ieder geval goed zijn als de auteurs daar wat dieper op in zouden gaan.
Los daarvan, ik denk ook belangrijker, is het zoals ik eerder had geschreven ook best plausibel dat covid-19-besmetting familiaire en locale verspreidingspatronen heeft, evenals de bloedgroepen een familiair en locaal patroon kunnen kennen, dat vervolgens zeker af kan wijken van de (verder sowieso onduidelijk gesampelde) steekproef van Xu et al. (En ook zeker als de groep zieken kleiner is (zoals bij de kleinere ziekenhuisgroepen), zijn dergelijke afwijkingen waarschijnlijker) Verder is het ook voorstelbaar dat bepaalde ethnische groepen minder waarschijnlijk naar een (bepaald) ziekenhuis gaan dan andere, maar om daar iets zinnigs over te zeggen moet je de gebruiken en situatie in Wuhan kennen natuurlijk.
Al met al is dit gewoon geen erg geslaagde onderzoeksopzet zou ik zeggen, nog helemaal los van statistiek.
Op het artikel is, zo op het eerste gezichte tenminste, nog wel het een en ander aan te merken, ook ten aanzien van de gekozen statistische methoden, en ik kan me voorstellen dat sommige reviewers ondanks de huidige omstandigheden aangaande covid-19 niet een (major) revision zouden voorstellen, maar eventueel gewoon een rejection.
We zullen zien. Het kan op zich wel de moeite waard zijn om de associatie bloedgroep-covid-19 nader te onderzoeken. Ik zou zeggen met een nieuw onderzoek, of in ieder geval met een betere verantwoording van de gekozen samplepopulatie.
[ Voor 12% gewijzigd door begintmeta op 20-03-2020 15:53 ]
/u/32368/crop694538950f5e0_cropped.png?f=community)
:strip_icc():strip_exif()/u/14/wildhagen60x60.jpg?f=community)
:strip_icc():strip_exif()/u/81396/profielfoto_69.jpg?f=community)
:strip_icc():strip_exif()/u/1254/crop62d7043e9eea6.jpg?f=community)
/u/12612/crop65b399f21bc43_cropped.png?f=community)
:strip_exif()/u/88107/crop6107159c924f6.gif?f=community)
:strip_icc():strip_exif()/u/91018/dgtw.jpg?f=community)
/u/81985/crop566b00b43645a.png?f=community)
:strip_icc():strip_exif()/u/154963/crop659be07d13f5a_cropped.jpg?f=community)
:strip_icc():strip_exif()/u/3228/crop5d113bdb41aeb_cropped.jpeg?f=community)