[Excel] Aantal diensten eerlijk verdelen obv beschikbaarheid

[PBGiebels]

Beste allen,

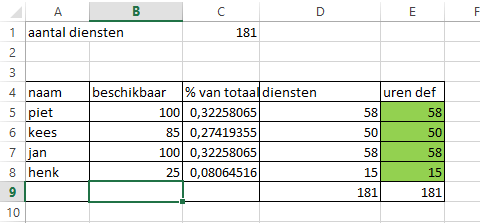
Ik heb 181 dagdiensten die ik moet verdelen onder 52 personen. Die personen hebben ieder een beschikbaarheidspercentage. Dat ziet er als volgt uit:

Piet: 100%
Kees: 85%
Jan: 100%
Henk: 25%
etc
etc

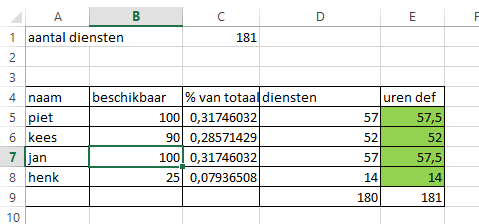
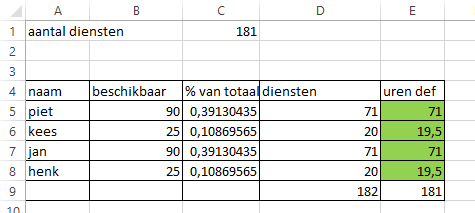
Is er een formule om een verdeling o.b.v. deze percentages te maken? Er kunnen alleen hele diensten worden verdeeld (dus er zijn 181 te verdelen eenheden).

Alvast hartelijk dank!

[HKLM_]

Wat is je verdeling je geeft aan dat Piet 100% is hoeveel uur of dagdiensten zou dit dan moeten zijn?

[Puch-Maxi]

Ik neem aan dat 100% 40 uren zijn en 1 dagdienst = 8 uur?

[PBGiebels]

Daar zit hem de crux. De 100% vertegenwoordigt geen exact aantal diensten, maar alleen een beschikbaarheidspercentage. 100% beschikbaarheid betekent dat je recht op meer diensten hebt dan iemand die minder beschikbaar is. Maar hoe dat principe vertaald kan worden naar de verdeling van diensten, dat is de vraag.

[MikeyMan]

Totaal aan percentages bij elkaar optellen en per persoon met zijn Eigen percentage vermenigvuldigen?

181 / Sum(total percentages) * percentage

oder etwas...

[ Voor 23% gewijzigd door MikeyMan op 07-03-2018 16:55 ]

[PBGiebels]

@Puch-Maxi 100% is een halfjaar dagelijks beschikbaar zijn (in dit geval dus 181 dagen). Een dienst beslaat een gehele dag.

[PBGiebels]

@MikeyMan dank je, maar dan kom je op getallen met decimalen uit en ik kan iemand bijvoorbeeld niet 3,6 diensten geven, alleen hele.

3,6 afronden gaat ook niet, want dan klopt het totaal niet meer.

[MikeyMan]

PBGiebels schreef op woensdag 7 maart 2018 @ 16:59:
@MikeyMan dank je, maar dan kom je op getallen met decimalen uit en ik kan iemand bijvoorbeeld niet 3,6 diensten geven, alleen hele.

3,6 afronden gaat ook niet, want dan klopt het totaal niet meer.

Hoe dacht je daaraan te ontkomen?
181 valt niet helemaal lekker te delen natuurlijk. Je zult of flexibel met de percentages om moeten gaan, of achteraf corrigeren.

[PBGiebels]

Ja, ik gok ook op de flexibele percentages...

[DirtyBird]

Misschien kun je met auctions werken? Waarbij het percentage hun 'bod' is op een dienst. Je hebt dan een homogene multi-unit auction. Daar zijn wel algoritmes voor.

Of misschien kun je een shortest path gebruiken om alle diensten optimaal te verdelen.

[PBGiebels]

Dat klinkt indrukwekkend, maar ik kan me er nog even niks bij voorstellen. Zijn beide principes kort uit te leggen?

[Lustucru]

Welkom op GoT.

Ik mis nog een en ander in de topicstart. je hebt het over formules. Bedoel je iets in Excel, ga je in Mathlab werken, of zoek je een algoritme wat je zelf wilt programmeren? Gaat het alleen om het eindresultaat of is dit echt een productievraag? Wat is eerlijk verdelen? Hoe ga je om met twee gelijkwaardige kandidaten? Wat is dan eerlijk? Op alfabetische volgorde?

Sowieso willen we dat je in je topicstart zelf aangeeft hoever je bent gekomen. Lees even Het algemeen beleid #topicplaatsen en vul je topicstart aan.

[Tens]

Even simpel gedacht op basis van jouw voorbeeld, en er van uitgaande dat er niemand 31,56% of 68,93% beschikbaar is is de volgende berekening een optie
100%,100%,85%,25%
is een verhouding van
20/20/17/5
Dus per periode van 62 diensten(20+20+17+5) is een 100% verdeling te maken op basis van beschikbaarheid.
Zie nu pas dat het om 52 personen gaat..... Dus zo simpel is het niet
die 181 diensten zijn dat 181 dagen, of bv 60 dagen waar 3 mensen dienst hebben? en hoe zit het met vakanties, voorkeuren voor werkdagen van de deeltijd werknemers?

[PBGiebels]

Hee Tens, dank voor je bericht.

Helaas komen alle percentages voor, ook met twee decimalen. Een dag is een dienst voor 1 persoon. Kortom: er zijn 181 eenheden te verdelen.

@Mod: ik heb nog geen enkele oplossing, omdat ik de theorie erachter eerst op orde wil hebben. Ik gebruik er alleen Excel voor, dus een formule of vba-code is wat ik zoek.

Uitgangspunt voor eerlijkheid is dat beschikbaarheid loont. Hoe hoger je beschikbaarheidspercentage, hoe meer diensten je krijgt. 100% beschikbaarheid betekent overigens 181 dagen beschikbaar zijn.

[Puch-Maxi]

Python:

#!/usr/bin/env python3
# Source: https://docs.python.org/3.4/library/random.html#examples-and-recipes

from collections import Counter
import itertools
import bisect
import random
random.seed(1)

def weighted_probabilities(werknemers):
    population = [val for val, cnt in werknemers for i in range(cnt)]
    return random.choice(population)

def cumulative_distribution(werknemers):
    choices, weights = zip(*werknemers)
    cumdist = list(itertools.accumulate(weights))
    x = random.random() * cumdist[-1]
    return choices[bisect.bisect(cumdist, x)]

def count_names(lst):
    for naam, dagen in sorted(Counter(lst).items()):
        print(naam, dagen)
    print()
    
def main():
    # Aannames:
    dagdiensten = 181

    # Beschikbaarheid werknemers
    werknemers = [
        ("Piet", 100),
        ("Kees", 85),
        ("Jan", 100),
        ("Henk", 25)
        ]

    a = []
    b = []
    for i in range(dagdiensten):
        a.append(weighted_probabilities(werknemers))
        b.append(cumulative_distribution(werknemers))

    # Resultaten
    count_names(a)
    count_names(b)

if __name__ == '__main__':
    main()

Henk 13
Jan 60
Kees 52
Piet 56

Henk 12
Jan 56
Kees 54
Piet 59

Lang niet ideaal, het buzzwoord is zelfroosteren .

[tinzarian]

Offtopic en niets bijdragend.

[ Voor 152% gewijzigd door Lustucru op 08-03-2018 01:05 ]

[PBGiebels]

@Puch-Maxi super! Bedankt. Ik merk dat ik veel te weinig kennis van zaken heb om jouw oplossingsrichting te begrijpen.

@tinzarian verder alles goed met je?

[Lustucru]

PBGiebels schreef op woensdag 7 maart 2018 @ 21:15:
@Mod: ik heb nog geen enkele oplossing, omdat ik de theorie erachter eerst op orde wil hebben. Ik gebruik er alleen Excel voor, dus een formule of vba-code is wat ik zoek.

Hoe zou je het aanpakken als je pen en papier had? Leg dat stap voor stap en dan willen we best meehelpen om dat in een stukje code in een taal naar wens te gieten.

[breew]

Als er alleen hele dagdiensten kunnen worden verdeeld; dan krijg je een probleem als het aantal dagdiensten per persoon niet op hele getallen uitkomt...

Mijn logica:

Verdeel alles procentueel, rond af naar 0 decimalen.

Er zijn nu drie mogelijkheden

1. het totaal komt uit op 181 --> klaar

2. het totaal komt uit onder 181 -->
a. geef iedereen met het hoogste beschikbaarheidspercentage een evenredig deel van de overgebleven diensten.
b. wordt dit een decimaal (bij verdeling over meerdere personen), laat ze dan onderling beslissen wie die dienst krijgt.

3. het totaal komt uit boven de 181:
a. geef iedereen met het laagste beschikbaarheidspercentage een evenredig deel van de overgebleven diensten minder.
b. wordt dit een decimaal (bij verdeling over meerdere personen), laat ze dan onderling beslissen wie die dienst moet inleveren.

In excel zou dit er zo uit kunnen zien:

voor rij 5:
C: % van totaal : 
        =B5/SOM($B$5:$B$8)
D: Aantal diensten, afgerond op 0 decimalen: 
        =AFRONDEN(C5*$C$1;0)
E. Aantal dagdiensten; indien som te  hoog -> minderen op de laagste, 
                       indien som te laag --> bijtellen bij de hoogste.
    (schrik niet...)
        =ALS(EN($D$9<$C$1;D5=MAX($D$5:$D$8));D5+1/AANTAL.ALS($D$5:$D$8;MAX($D$5:$D$8));ALS(EN($D$9>$C$1;D5=MIN($D$5:$D$8));D5-1/AANTAL.ALS($D$5:$D$8;MIN($D$5:$D$8));D5))

resultaat indien totaal (D9) ok:


resultaat indien totaal (D9) te laag:


resultaat indien totaal (D9) te hoog:

[PBGiebels]

@breew thumbs up!! Dit zou em zomaar eens kunnen worden. Ook jouw oplossing bij overschat of tekort.

Bedankt!

[F_J_K]

offtopic:
Je kunt die thumb up ook geven via de knop. Als @breew de gewenste oplossing gaf, kan je zijn post ook als antwoord aanduiden. Nuttig voor andere mensen die min of meer dezelfde vraag hebben en dus ook dit topic tegenkomen bij zoeken.

Ik zet ook in dat kader nog even Excel in de topictitel. Bij 'Een aantal diensten eerlijk verdelen o.b.v. beschikbaarheid' dacht ik aan bijv. spreiden over verschillende webservers of zo

[Puch-Maxi]

breew schreef op donderdag 8 maart 2018 @ 09:40:
Als er alleen hele dagdiensten kunnen worden verdeeld; dan krijg je een probleem als het aantal dagdiensten per persoon niet op hele getallen uitkomt...

Dat lijkt mij ook de beste oplossing

Python:

#!/usr/bin/env python3
def main():
    dagdiensten = 181
    werknemers = {
        "Piet" : 100,
        "Kees" : 85,
        "Jan" : 100,
        "Henk" : 25,
        }

    som = sum(werknemers.values())
    totaal = 0

    for naam, beschikbaarheid in werknemers.items():
        percentage = beschikbaarheid / som
        dagen = round(percentage * dagdiensten)
        print(naam, dagen)
        totaal += dagen

    print("\nTotaal aantal dagen:", totaal)
    
if __name__ == '__main__':
    main()

Piet 58
Kees 50
Jan 58
Henk 15

Totaal aantal dagen: 181

[Lustucru]

PBGiebels schreef op woensdag 7 maart 2018 @ 21:15:
Hee Tens, dank voor je bericht.

Helaas komen alle percentages voor, ook met twee decimalen. Een dag is een dienst voor 1 persoon. Kortom: er zijn 181 eenheden te verdelen.

@Mod: ik heb nog geen enkele oplossing, omdat ik de theorie erachter eerst op orde wil hebben. Ik gebruik er alleen Excel voor, dus een formule of vba-code is wat ik zoek.

Uitgangspunt voor eerlijkheid is dat beschikbaarheid loont. Hoe hoger je beschikbaarheidspercentage, hoe meer diensten je krijgt. 100% beschikbaarheid betekent overigens 181 dagen beschikbaar zijn.

Voor de theorie kun je te rade gaan bij verkiezingen: ook daar wordt een variabele grootheid (stemmen / beschikbaarheidspercentage) naar rato verdeeld over een verzameling integers (zetels / resp diensten).

Wat dan eerlijk is, blijft een punt van discussie. Het ene systeem bevoordeelt grote partijen (hoge beschikbaarheid), het andere kleinere, en sommige geven over de hele linie 'oneerlijkheden'. Maar de variant die @breew geeft vind je in het wild nog niet terug.

De meeste varianten werken met restzetelverdeling. In jouw geval: verdeel eerst de diensten met afronden.naar.beneden. De diensten die overblijven verdeel je of:
- via de grootste rest: degenen die de meeste beschikbaarheid overhouden krijgen een extra dienst
of
-via het grootste gemiddelde: degenen die na het toekennen van een restdienst de grootste gemiddelde beschikbaarheid hebben krijgen die dienst.

Maar er zijn ook varianten die eerst een sleutel bepalen en dan de diensten verdelen via delerreeksen. En werkelijk waar: elk systeem kan andere verdelingen opleveren.