hoihoi
Ik ben zoals elk jaar weer bezig met de NBV-puzzel en daar zit wel een geinige opgave in die ik wilde programmeren:
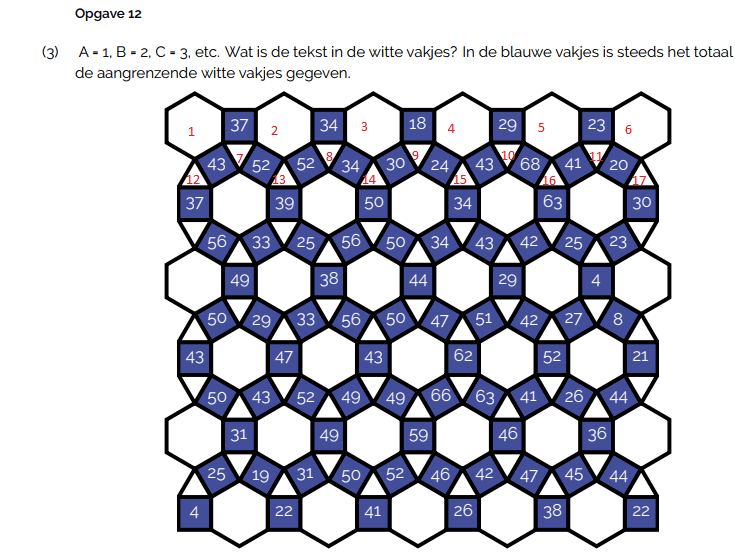
Nu kun je hier natuurlijk een vergelijking schrijven in de vorm van:
37 = w1 + w2 + w7
43 = w1 + w7 + 12
et cetera et cetera. Dan is het handig om rechts in het midden van de puzzle te beginnen (daar vind je 4x 1). Hierbij is wN de waarde van veld N. Ik verwacht dat dit initieel best wel veel opties oplevert , maar gezien er 88 velden zijn dit aantal fors inkakt.
Dit uitwerken vind ik een leuke oefening voor mezelf; ik heb in het verleden dingen met allerlei gare SAT-solvers gedaan (Alloy ed) maar eigenlijk nooit met Python. Ik ben me er ook terdege van bewust dat dit soort middelen niet noodzakelijk is voor het oplossen van de puzzle.
Enige waar ik me zorgen om maak is dat het aantal opties uit de hand loopt. Als je gewoon wat arrays aanmaakt en slim gaat reduceren houdt het vrij snel op. Dus wellicht is er een library die dit goed aan kan pakken. Iemand tips?
Nu wilde ik eens naar numpy voor de vergelijkingen kijken, maar ook naar sympy. Heeft iemand nog wat libs of algemene trucs hiervoor?
Ik ben zoals elk jaar weer bezig met de NBV-puzzel en daar zit wel een geinige opgave in die ik wilde programmeren:

Nu kun je hier natuurlijk een vergelijking schrijven in de vorm van:
37 = w1 + w2 + w7
43 = w1 + w7 + 12
et cetera et cetera. Dan is het handig om rechts in het midden van de puzzle te beginnen (daar vind je 4x 1). Hierbij is wN de waarde van veld N. Ik verwacht dat dit initieel best wel veel opties oplevert , maar gezien er 88 velden zijn dit aantal fors inkakt.
Dit uitwerken vind ik een leuke oefening voor mezelf; ik heb in het verleden dingen met allerlei gare SAT-solvers gedaan (Alloy ed) maar eigenlijk nooit met Python. Ik ben me er ook terdege van bewust dat dit soort middelen niet noodzakelijk is voor het oplossen van de puzzle.
Enige waar ik me zorgen om maak is dat het aantal opties uit de hand loopt. Als je gewoon wat arrays aanmaakt en slim gaat reduceren houdt het vrij snel op. Dus wellicht is er een library die dit goed aan kan pakken. Iemand tips?
Nu wilde ik eens naar numpy voor de vergelijkingen kijken, maar ook naar sympy. Heeft iemand nog wat libs of algemene trucs hiervoor?
[ Voor 6% gewijzigd door Boudewijn op 21-12-2017 22:44 ]
:strip_icc():strip_exif()/u/105199/crop5cb76c6d18020_cropped.jpeg?f=community)
/u/22274/banaan60x60.png?f=community)
:strip_icc():strip_exif()/u/671790/crop56cef352f3117_cropped.jpeg?f=community)
/u/399457/crop5a9e7c5ce5925_cropped.png?f=community)
:strip_icc():strip_exif()/u/634276/crop619ebb940edfb.jpg?f=community)