Wat een leuk probleempje om wat vba-werk op los te laten.
Ik ben uitgegaan van de getallen uit je startpost, Art1 = 4.68, art2 = 10.8.
Mijn code vindt in totaal 7 optimale oplossingen voor de combinatie van beide artikelen (allen met een restwaarde van 0,08 tov 1000)...
Wat doet de code functioneel:
- hoog de hoeveelheid van artikel 1 steeds op met 1, net zo lang tot je het maximum van 1000 overschrijdt
- bepaal hoeveel van artikel 2 je nodig hebt om zo dicht mogelijk bij 1000 te komen, geven de hoeveelheid van artikel 1 (1.)
- bepaal hoe ver je van 1000 af zit met bovenstaande combinatie van artikel 1 en artikel 2 (1. en 2.)
- zit je dichter bij 1000 dan de tot nu toe beste oplossing, dan is deze combinatie van 1 en 2 het beste
- zit je net zo ver van 1000 als de tot nu toe beste oplossing, voeg de combinatie van 1 en 2 dan toe aan de verzameling met beste oplossingen
- ga terug naar 1.
- als de grens van 1. is bereikt, toon de verzameling met beste oplossingen
Uitkomst van onderstaande code:
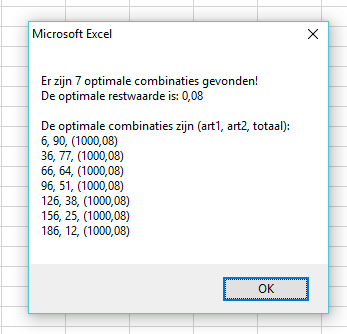
Stel je het maximum in op 250, dan krijg je het volgende:
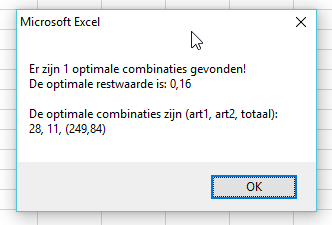
Probeer eerst te begrijpen wat de code doet, voordat je hem gaat implementeren! Mijn code is slechts één aanvliegroute, die vrij 'dom' door mogelijke combinaties heen akkert..
Het kan allemaal slimmer, en sneller, maar de code is volgens mij op deze manier goed leesbaar.
Visual Basic:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
| Option Explicit
Sub OptimaliseerDieHandel()
'uitgangspunten
' - 2 artikelen (artikel 1 en artikel 2)
' - eerste artikel (artikel 1) is het lichtst
'declaratie
Dim dblArt1 As Double 'de prijs/gewicht/etc.. van het eerste artikel
Dim dblArt2 As Double 'de prijs/gewicht/etc vna hte tweede artikel
Dim lonMaximum As Long 'het maximum wat je zo dicht mogelijk wilt benaderen
Dim lonAantalArt1 As Long 'aantal van artikel 1
Dim lonAantalArt2 As Long 'aantal van artikel 2
Dim dblSom As Double 'som van de waarde van het totaal van artikel 1 en het totaal van artikel 2
Dim dblRest As Double 'de restwaarde (lonMaximum - dblSom)
Dim dblRestOptimum As Double 'de kleinste tot nu toe bekende restwaarde (het optimum dus)
Dim i As Long 'lusteller
Dim intOptimum As Integer 'hoeveel optimale combinaties van artikel 1 en 2 zijn bekend
Dim arrArt1() As Long 'array met optimale hoeveelheden van artikel 1
Dim arrArt2() As Long 'array met optimale hoeveelheden van artikel 2
Dim dblTotaal As Double 'waarde van de combinatie artikel 1 en artikel 2
Dim strOptimum As String 'string met het eindantwoord
'initialisatie
dblArt1 = 4.68
dblArt2 = 10.8
lonMaximum = 1000
dblRest = lonMaximum
dblRestOptimum = lonMaximum
'doorloop zo vaak als dat het lichtste artikel in het maximum past (verdeling = 100%-0%)
For i = 1 To Round((lonMaximum / dblArt1) + 1, 0)
lonAantalArt1 = i
'bepaal de hoeveelheid van artikel 2, zodat het resultaat zo dicht mogelijk bij lonMaximum ligt.
lonAantalArt2 = Round((lonMaximum - lonAantalArt1 * dblArt1) / dblArt2, 0)
'aangezien we ook iets boven het maximum mogen uitkomen, ga na of je het aantal van artikel2 met 1 op kunt hogen voor een beter resultaat
If Abs(lonMaximum - (lonAantalArt1 * dblArt1 + lonAantalArt2 * dblArt2)) > Abs(lonMaximum - (lonAantalArt1 * dblArt1 + (lonAantalArt2 + 1) * dblArt2)) Then
'levert dat ene beter resultaat op? dan het aantal van artikel2 met 1 ophogen
lonAantalArt2 = lonAantalArt2 + 1
End If
'rest bepalen. afronden is nodig, omdat we anders tegen floating point errors aanlopen
dblRest = Round(Abs(lonMaximum - (lonAantalArt1 * dblArt1 + lonAantalArt2 * dblArt2)), 3)
'vergelijk dblRest nu met de optimale restwaarde (die zo dicht mogelijk bij 0 moet liggen)
Select Case dblRest
'als de nieuwe restwaarde kleiner is dat het tot nu toe bekende optimum
Case Is < dblRestOptimum
'arrays met optimale combinaties leegmaken
ReDim arrArt1(0 To 0)
ReDim arrArt2(0 To 0)
'arrays vullen met de nieuwe optimale waarden
arrArt1(0) = lonAantalArt1
arrArt2(0) = lonAantalArt2
'aantal optimalewaarden resetten naar 0 (dit is een foefje, om de arrays bij meerdere optima te kunnen vullen)
intOptimum = 0
'de huidige rest is de nieuwe optimale waarde
dblRestOptimum = dblRest
'als de rest gelijk is aan het tot nu toe bekende optimum
Case Is = dblRestOptimum
'er is een extra optimum gevonden, teller met 1 ophogen
intOptimum = intOptimum + 1
'arrays met optima uitbreiden naar het aantal optimale combinaties
ReDim Preserve arrArt1(0 To intOptimum)
ReDim Preserve arrArt2(0 To intOptimum)
'laatste entry in de arrays vullen met de nieuwe combinatie optimale waarden
arrArt1(intOptimum) = lonAantalArt1
arrArt2(intOptimum) = lonAantalArt2
Case Else
End Select
Next i
'weergeven van een venster met de optimale combinaties
'iniktialiseren van de string
strOptimum = "Er zijn " & intOptimum + 1 & " optimale combinaties gevonden!" & vbCrLf & "De optimale restwaarde is: " & dblRestOptimum & vbCrLf & vbCrLf & _
"De optimale combinaties zijn (art1, art2, totaal):" & vbCrLf
'vullen van de string met de optimale waarden
For i = LBound(arrArt1) To UBound(arrArt1)
dblTotaal = arrArt1(i) * dblArt1 + arrArt2(i) * dblArt2
strOptimum = strOptimum & arrArt1(i) & ", " & arrArt2(i) & ", (" & dblTotaal & ")" & vbCrLf
Next i
'toon de string
MsgBox (strOptimum)
'KLAAR!!! KOFFIETIJD!!
End Sub |
[
Voor 10% gewijzigd door
breew op 28-11-2017 12:14
]
:strip_icc():strip_exif()/u/85308/mirko.jpg?f=community)
/u/72820/crop66f3ae5a89071.png?f=community)

