ik ben bezig met een html5 demo optica. ik wil een lens simuleren als je het brandpunt veranderd Dit is geen huiswerk opdracht maar gewoon voor de hobby  , heb nog vakantie en kan het mijn wiskunde docent ook niet vragen
, heb nog vakantie en kan het mijn wiskunde docent ook niet vragen
het probleem is dat de radius onbekend is ipv het brandpunt. De overige variabelen zijn constanten.
ik wil R als functie van f hebben
Op Wikipedia staat een formule waarmee je het brandpunt kan uitrekenen als de radius bekend is. (lenzenmakersformule)
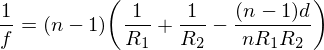
De lens in mijn demo is symetrish, dus r1=r2, wat de formule wat simpeler maakt
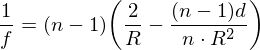
Maar deze formule is in de verkeerde richting ik wil R=F*blabla ipv F=R*blabla
zelf heb ik het geprobeerd op te lossen maar ik heb niet het idee dat ik verder kom
mijn berekening:
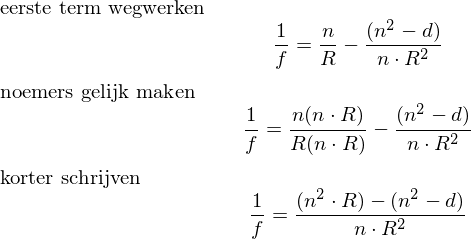
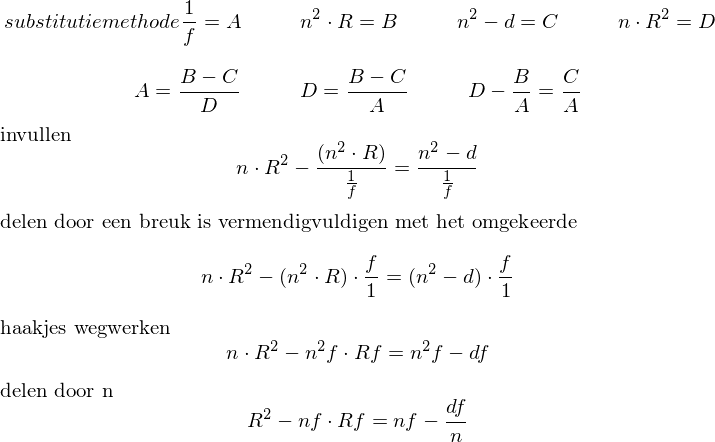
Maar hierna weet ik het niet meer. ik krijg de F en R maar niet van elkaar gescheiden
kan iemand mij helpen?
het probleem is dat de radius onbekend is ipv het brandpunt. De overige variabelen zijn constanten.
ik wil R als functie van f hebben
Op Wikipedia staat een formule waarmee je het brandpunt kan uitrekenen als de radius bekend is. (lenzenmakersformule)
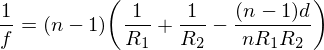
De lens in mijn demo is symetrish, dus r1=r2, wat de formule wat simpeler maakt
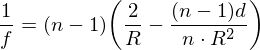
Maar deze formule is in de verkeerde richting ik wil R=F*blabla ipv F=R*blabla
zelf heb ik het geprobeerd op te lossen maar ik heb niet het idee dat ik verder kom
mijn berekening:
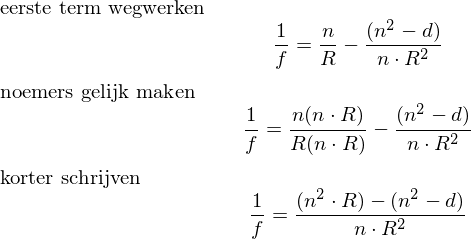
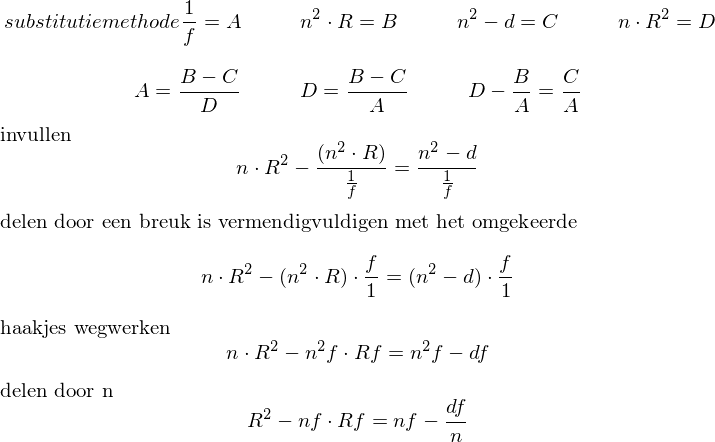
Maar hierna weet ik het niet meer. ik krijg de F en R maar niet van elkaar gescheiden
kan iemand mij helpen?
ora et labora
:strip_icc():strip_exif()/u/373647/b1aa8209a437bf987cf066823c044f0a.jpeg?f=community)
:strip_exif()/u/242341/crop55d72c2ca29b1.gif?f=community)
:strip_icc():strip_exif()/u/46486/RayBan.jpg?f=community)
/u/79923/DUT11.png?f=community)
:strip_exif()/u/306933/ezgif.com-optimize.gif?f=community)











