Niet echt een programmeervraag, meer een wiskundig vraagstuk, maar denk dat het hier toch het best op z'n plaats is op GoT.
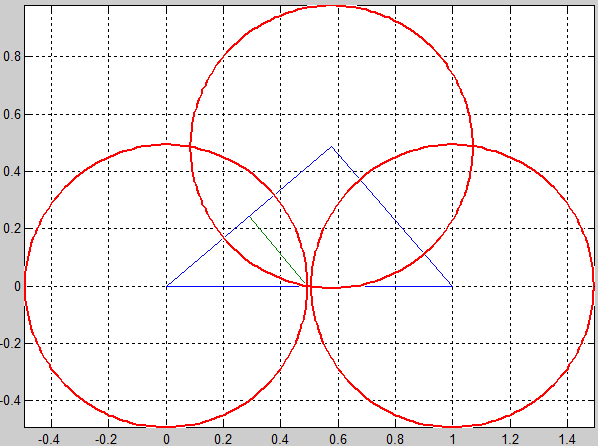
Gedefinieerd zijn drie punten (als x en y waarde). Je verbindt die drie punten en krijgt een driehoek, waarvan je dan natuurlijk alle drie de zijdes weet. Wat ik vervolgens wil weten is wat de kleinste straal is waarbij je met drie gelijke cirkels, één om elk hoekpunt, het gehele oppervlak van de driehoek kan bedekken.
Wat ik tot nu toe heb is het volgende:
langste zijde / 4 < r ≤ langste zijde / √3
Wat vrij gemakkelijk te beredeneren is:
De ondergrens, kwart van de langste zijde, heb je wanneer de drie punten op één lijn liggen met gelijke afstand tussen het middelste punt en de punten aan de uiteinden van het lijnstuk. Dus een gelijkbenige driehoek met één hoek van 180° en twee van 0°. Doordat de driehoek dan eigenlijk geen driehoek is, telt dit geval zelf niet mee. Dus de straal van de cirkels is groter dan een kwart van langste zijde
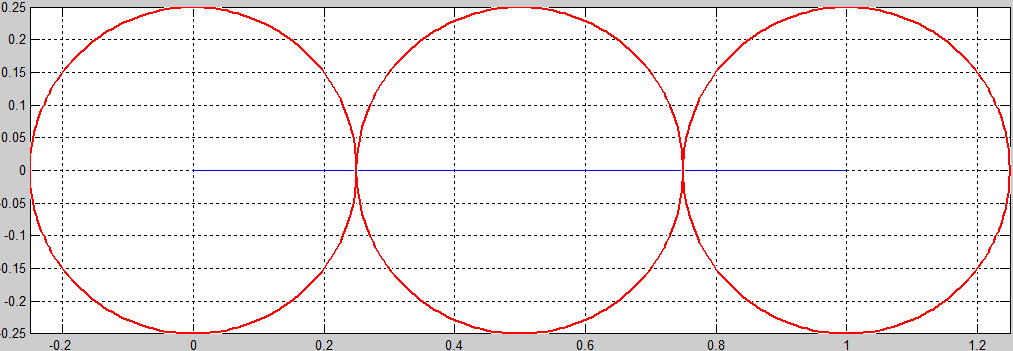
De bovengrens, langste zijde gedeeld door √3, heb je bij een gelijkzijdige driehoek (waarbij alle zijdes natuurlijk gelijk zijn en het dus niet uitmaakt welke je pakt). Dan is het namelijk gelijk aan de afstand van een hoekpunt tot het zwaartepunt van de driehoek.
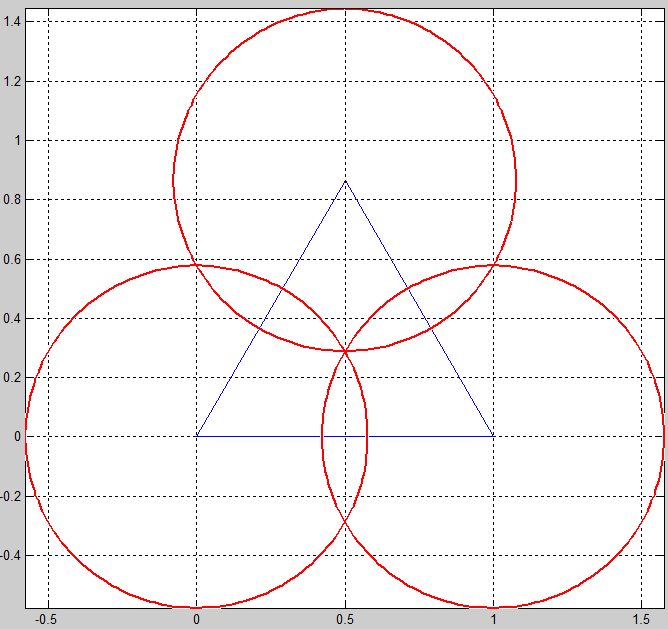
Wat me tot nu toe alleen niet gelukt is, is het bedenken van een algemene formule voor dit probleem. Zoeken op internet heeft ook niks opgeleverd. Zodra je gaat zoeken op iets met cirkels en driehoeken krijg je eigenlijk alleen maar resultaten over de ingeschreven en omgeschreven cirkels van een driehoek.
Hebben jullie enig idee hoe ik de straal van de cirkels bereken op basis van de lengtes van drie zijdes van de driehoek?
Gedefinieerd zijn drie punten (als x en y waarde). Je verbindt die drie punten en krijgt een driehoek, waarvan je dan natuurlijk alle drie de zijdes weet. Wat ik vervolgens wil weten is wat de kleinste straal is waarbij je met drie gelijke cirkels, één om elk hoekpunt, het gehele oppervlak van de driehoek kan bedekken.
Wat ik tot nu toe heb is het volgende:
langste zijde / 4 < r ≤ langste zijde / √3
Wat vrij gemakkelijk te beredeneren is:
De ondergrens, kwart van de langste zijde, heb je wanneer de drie punten op één lijn liggen met gelijke afstand tussen het middelste punt en de punten aan de uiteinden van het lijnstuk. Dus een gelijkbenige driehoek met één hoek van 180° en twee van 0°. Doordat de driehoek dan eigenlijk geen driehoek is, telt dit geval zelf niet mee. Dus de straal van de cirkels is groter dan een kwart van langste zijde

De bovengrens, langste zijde gedeeld door √3, heb je bij een gelijkzijdige driehoek (waarbij alle zijdes natuurlijk gelijk zijn en het dus niet uitmaakt welke je pakt). Dan is het namelijk gelijk aan de afstand van een hoekpunt tot het zwaartepunt van de driehoek.

Wat me tot nu toe alleen niet gelukt is, is het bedenken van een algemene formule voor dit probleem. Zoeken op internet heeft ook niks opgeleverd. Zodra je gaat zoeken op iets met cirkels en driehoeken krijg je eigenlijk alleen maar resultaten over de ingeschreven en omgeschreven cirkels van een driehoek.
Hebben jullie enig idee hoe ik de straal van de cirkels bereken op basis van de lengtes van drie zijdes van de driehoek?

:strip_exif()/u/3157/sail4L_S70.gif?f=community)


/u/107051/jeroenmadtrix60.png?f=community)
:strip_icc():strip_exif()/u/35767/images.jpg?f=community)