Netto kleurdiepte berekenen

[Kid Jansen]

Ik had laatst een interessante gedachte: "hoe bereken je netto kleurdiepte?"

De uitleg:

Kleur kan worden opgedeeld in twee elementen, chromaticity en luminance (ik gebruik even de Engelse termen, omdat ik de vertaling van die eerste naar het Nederlands crap vind).

Chromaticity bepaalt de verhoudingen tussen de helderheid van de verschillende golflengtes waar een kleur uit is samengesteld en Luminance bepaalt de helderheid van de kleur als geheel.

Een aantal voorbeelden:

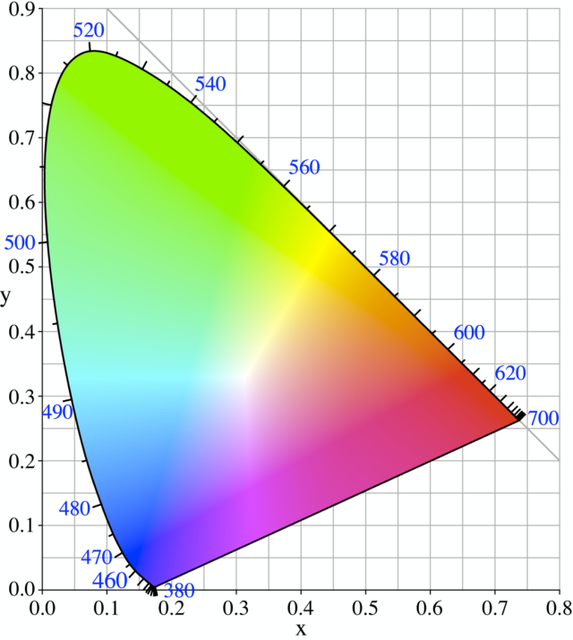
0;0;0, 1;1;1, 2;2;2,..., 61;61;61, 62;62;62, 63;63;63 zijn allemaal grijswaarden, deze hebben allemaal dezelfde chromaticity (namelijk die van het witpunt, meestal D65, met de coördinaten Wx 0.313 en Wy 0.329 in het CIE 1931 xy chromaticity diagram), maar de helderheid is verschillend.

Je zou eventueel zwart (0;0;0) nog als een uitzondering kunnen zien, want die heeft eigenlijk geen chromaticity, zolang je uitgaat van een perfect licht blokkerend paneel. Immers, als er geen licht is, dan kan het ook geen kleur hebben. In de praktijk is een paneel echter nooit perfect blokkerend, dus is 'zwart' een kleur.

Een andere voorbeeld is 1;0;0, 2;0;0,..., 62;0;0, 63;0;0 (wederom allemaal dezelfde chromaticity, namelijk de extreme waarde van rood, alleen de helderheid verschilt).

Maar natuurlijk ook 21;7;5, 42;14;10, 63;21;15 (allemaal dezelfde onderlinge verdeling, dus dezelfde chromaticity, alleen helderheid verschilt).

Aangezien een paneel zowel de chromaticity (onderlinge verhouding in helderheid tussen de drie subpixels) en de helderheid (waarschijnlijk ongeveer de gemiddelde helderheid van de drie subpixels) moet regelen, spreekt het voor zich dat je dus heel veel mogelijkheden kwijt bent aan alleen helderheid, omdat ze dezelfde onderlinge verhoudingen in helderheid hebben.

Ik heb nu 6 bit voorbeelden gebruikt, waarbij rood, groen en blauw dus elk 64 niveaus hebben, goed voor in totaal 262144 kleurniveaus.

Nu zou ik graag willen weten hoe ik het aantal mogelijkheden bereken waarbij er minimaal één andere mogelijkheid is met dezelfde onderlinge verhouding (oftewel een gemeenschappelijke deler (uit de verzameling natuurlijke getallen en groter dan 1)).

Zodat ik het aantal daarvan kan aftrekken van 262144 en dan dus weet hoeveel kleurniveaus een verschillende chromaticity opleveren bij een 6 bit paneel.

Ik neem aan dat dit wel met een algemene manier kan, dus dat de totale kleurdiepte niet uitmaakt, mocht dat wel zo zijn, dan zijn de enige relevante kleurdieptes 6, 8, 10, 12 en 16 bit per primaire kleur (subpixel).

Voor zover ik het me van de middelbare school kan herinneren moet dit prima op te lossen zijn met wat standaard kansrekening, maar ik kom er even niet uit hoe en ik heb eigenlijk ook geen idee waar ik op moet zoeken. Dus als iemand mij in ieder geval in de goede richting zou kunnen sturen zou dat al heel veel helpen.


NB ik had dit eerst gepost in \[Wiskunde/excel] area van overlappende driehoeken berekenen, maar het leek me toch handiger om er een nieuw topic voor aan te maken, omdat het raakvlak met dat vraagstuk toch niet zo heel groot was.

[voodooless]

Voor 6 bits kun je dat nog redelijk eenvoudig op een brute force manier doen.
Bereken voor iedere mogelijke kleur de verhouding, en tel het totaal aantal unieke verhoudingen.

Als je naar meer dan 6 bits gaat het allemaal wel erg lang duren en komst het veel memory... Daar zijn vast slimmere truckjes voor Maar wiskunde is niet mijn sterkste kant, dus daar waag ik me niet aan.

[Kid Jansen]

8 bit zal ook nog wel lukken denk ik, 10, 12 en 16 wordt een ander verhaal.

[MLM]

Wat bedoel je nou met "hoeveel kleurniveaus een verschillende chromaticity opleveren"
Het aantal chromaticity waarden waarvoor slechts 1 kleurniveau bestaat?
Het gemiddelde aantal kleurniveaus per chromaticity?
Het aantal unieke chromaticity waarden in het bereik?

Jouw voorgestelde algoritme berekend het eerste, maar volgens mij zoek je het antwoord op 1 van de andere 2, en dat ga je zo niet vinden

[Kid Jansen]

chromaticity is de verhouding tussen rood, groen en blauw in het geval van beeldschermen, dus ik wil het aantal unieke verhoudingen weten.

[Anoniem: 303530]

Ik snap niet precies wat je wilt, als ik het goed begrijp wil je weten voor een bepaalde kleur, hoeveel keer die kleur bestaat met een andere helderheid.

bijvoorbeeld: de kleur (1,2,0) komt in totaal 32 (of 31?) keer voor in verschillende helderheid
Is dat niet bizar simpel uit te rekenen door de LCM te pakken van die 3 getallen, en dat vervolgens door de kleurdiepte (=63 of 64, even uitproberen) te delen en naar beneden af te ronden?

[Kid Jansen]

Nee precies andersom, ik wil het aantal unieke verhoudingen.

Dus in jou voorbeeld zijn er 31 verschillende helderheden voor de chromaticitywaarde 1;2;0, namelijk 1;2;0, 2;4;0, 3;6;0,..., 29;58;0, 30;60;0, 31;62;0.

Maar aangezien die allemaal dezelfde verhouding hebben tellen die 31 maar als één chromaticitywaarde, wat ik wil weten is het aantal chromaticitywaarden (dus het aantal unieke verhoudingen tussen rood, groen en blauw).

[Shagura]

Ok hier stond wat debiel gereutel...

[ Voor 96% gewijzigd door Shagura op 09-02-2011 15:41 ]

[Anoniem: 303530]

ofwel: het aantal unieke waarden van(x,y,z) / LCM(x₂, y₂, z₂) waar 0 <= (x, y, z) <= 2ⁿ
en waar x₂ = max(1,x)

Zo moeilijk is dat toch niet?

[MLM]

een snelle poging van mij komt op 249255 van de 262144 zijn uniek
als dat klopt, dan kan het algoritme ook de andere wel berekenen

edit: zie volgende post

[ Voor 11% gewijzigd door MLM op 09-02-2011 16:10 ]

[Kid Jansen]

Shagura schreef op woensdag 09 februari 2011 @ 15:26:
...Er is vast wel een kleurenmodel te vinden waarbij de chromaticiteit als 2 dimensies uit te drukken is en luminance als derde met wat wiskunde om deze om te rekenen naar het RGB-model. Is dat niet gewoon HSL?

Geen idee wat HSL is, maar ja, die bestaat inderdaad. Dat is het CIE 1931 xy chromaticity diagram. Dat geeft het chromaticity deel weer van de CIE 1931 xyY kleurruimte, waarin Y de helderheid is en xy de chromaticity. Die CIE 1931 xyY kleurruimte is een kleurruimte die is afgeleid van de CIE 1931 XYZ kleurruimte.

@ MLM: dat lijkt mij eerlijk gezegd nogal veel, hoe kom je daar precies op?

[ Voor 5% gewijzigd door Kid Jansen op 09-02-2011 15:48 ]

[Shagura]

Ik snap er nog steeds weinig van dus misschien moet ik maar gewoon stoppen met blaten, maar aangezien kleuren altijd 3-dimensionaal zijn en chromaticiteit 2 dimensies is is het aantal chromaticiteiten toch altijd 2 keer je bitrate van 1 dimensie? Als je kleuren uitdrukt met 6 bits per kleur is het aantal chromaticiteiten 64*64 = 4096...

HSL is gewoon een ander model om kleuren uit te drukken, waarbij volgens mij H en S samen de chromaticiteit zijn en lightness ruwweg de luminance. Het leek mij alleen makkelijk omdat je daarmee de chromaticiteit direct als 2 dimensies hebt zonder deze te hoeven afleiden. Daarnaast is hij 1 op 1 converteerbaar naar RGB.

Geen idee wat die CIE kleurenruimtes hier verder mee te maken hebben. Deze ruimtes drukken alle zichtbare kleuren uit, maar ook niet bestaande kleuren en kleuren die bijvoorbeeld niet eens door een monitor geproduceerd kunnen worden. RGB en HSL zijn hier ook gewoon subsets van.

[ Voor 42% gewijzigd door Shagura op 09-02-2011 16:16 ]

[MLM]

kan dit kloppen?

uniekheid:
6 bits: 176267 van de 262144 (67%)
8 bits: 12658178 van de 16777216 (75%)
10 bits: 862308289 van de 1073741824 (80%)
12 bits: 57524330094 van de 68719476736 (83%)

[ Voor 165% gewijzigd door MLM op 09-02-2011 17:14 ]

[Kid Jansen]

Dat klinkt een heel stuk aannemelijker, zowel de percentages op zich, als de toename in uniekheid naarmate de kleurdiepte groter is.

Hoe heb je dit berekend?

[MLM]

bruteforcen

code:

N = aantal bits (input)
uniek = 0
voor alle combinaties van [R G B] in bereik 0 t/m 2^N-1
{
  X = intersection(delers(R), delers(G), delers(B))
  als(X is leeg) uniek := uniek + 1
}

delers(0) gedefinieerd als "alles"
ook gelijk de reden waarom ik bits=16 niet berekend heb, dat gaat 4096 keer langer duren dan bits=12, meer dan een dag waarschijnlijk

[ Voor 28% gewijzigd door MLM op 09-02-2011 17:44 ]

[Klaasvaak]

Bij 6 bits 2/3 deel, 8 bits 3/4, 10 bits 4/5 en 12 bits 5/6. Bij 16 bits dan waarschijnelijk 7/8 deel?
Zal dan ook wel wiskundig op te lossen zijn.

[Kid Jansen]

Als 12 bits meer dan 21 seconden duurt wel ja. Ik ben in ieder geval blij dat ik voor 6 t/m 12 bits al een antwoord heb. Maar ik ben ook geïnteresseerd in een algebraïsche oplossing, ik denk dat dat namelijk ook niet zo moeilijk kan zijn, maar ik heb het idee dat ik het gewoon over het hoofd zie.

[ Voor 82% gewijzigd door Kid Jansen op 09-02-2011 18:31 ]

[Soultaker]

@MLM: weet je zeker dat dat klopt? Ik kom met semi-slimme bruteforce op de volgende waarden:

code:

 1:                7 /               8 = 0.875000000
 2:               49 /              64 = 0.765625000
 3:              415 /             512 = 0.810546875
 4:             3313 /            4096 = 0.808837891
 5:            27133 /           32768 = 0.828033447
 6:           217021 /          262144 = 0.827869415
 7:          1742299 /         2097152 = 0.830792904
 8:         13936093 /        16777216 = 0.830655873
 9:        111613717 /       134217728 = 0.831586994
10:        892986613 /      1073741824 = 0.831658592
11:       7145445727 /      8589934592 = 0.831839364
12:      57162518101 /     68719476736 = 0.831824118
13:     457336049863 /    549755813888 = 0.831889429
14:    3658704710983 /   4398046511104 = 0.831893137
15:   29269975102681 /  35184372088832 = 0.831902727
16:  234159670586299 / 281474976710656 = 0.831902265

(Waarbij rgb(0,0,0) niet meegeteld wordt.) Het mooie patroon dat Klaasvaak aanwijst verdwijnt bij mij. (Lijkt me ook niet dat het zó simpel is, eerlijk gezegd.) Als mijn antwoord klopt, weet ik nog wel een manier om het efficiënter uit te rekenen.

edit:
Het lijkt A090025(2^diepte-1) te zijn op OEIS. Daar staat ook code om 'm relatief handig uit te rekenen.

[ Voor 67% gewijzigd door Soultaker op 09-02-2011 19:44 ]

[Anoniem: 303530]

Wat klaasvaak zegt ziet er erg logisch uit, met 4 Bit kleurdiepte heb je dan 1/2. Al klopt het niet helemaal (waarschijnlijk omdat er bepaalde waarden zijn die niet in het patroon vallen.

alle waarden zijn n.l. net iets groter dan 3/4 en 4/5 enz.

[Kid Jansen]

Anoniem: 303530 schreef op woensdag 09 februari 2011 @ 18:29:
Wat klaasvaak zegt ziet er erg logisch uit, met 4 Bit kleurdiepte heb je dan 1/2. Al klopt het niet helemaal (waarschijnlijk omdat er bepaalde waarden zijn die niet in het patroon vallen.

alle waarden zijn n.l. net iets groter dan 3/4 en 4/5 enz.

Inderdaad, het is niet precies 2/3, 3/4, 4/5 en 5/6:

0,672405243
0,754486203
0,803087176
0,837089175

Het is dus iedere keer net iets groter dan 2/3, 3/4, 4/5 en 5/6 en wel met respectievelijke de volgende factoren:

1,008607864
1,005981604
1,00385897
1,00450701

Wat ik alleen raar vind is dat die factor bij die eerste drie duidelijk een dalende lijn vormt, maar bij 12 bits ineens weer omhoog gaat.

[MLM]

Soultaker schreef op woensdag 09 februari 2011 @ 18:28:
@MLM: weet je zeker dat dat klopt? Ik kom met bruteforce op de volgende waarden:

code:

 1:           7 /          8 = 0.875000000
 2:          49 /         64 = 0.765625000
 3:         415 /        512 = 0.810546875
 4:        3313 /       4096 = 0.808837891
 5:       27133 /      32768 = 0.828033447
 6:      217021 /     262144 = 0.827869415
 7:     1742299 /    2097152 = 0.830792904
 8:    13936093 /   16777216 = 0.830655873
 9:   111613717 /  134217728 = 0.831586994
10:   892986613 / 1073741824 = 0.831658592

(Waarbij rgb(0,0,0) niet meegeteld wordt.) Het mooie patroon dat Klaasvaak aanwijst verdwijnt bij mij. (Lijkt me ook niet dat het zó simpel is, eerlijk gezegd.) Als mijn antwoord klopt, weet ik nog wel een manier om het efficiënter uit te rekenen.

Ik had inderdaad een foutje, de collectie delers(x) zat geen x in, dus mijn resultaten waren fout (alles met een 1 erin telde hij altijd goed )
Mijn resultaten zijn nu exact jouw resultaten + 1, (ik tel [0,0,0]) wel als uniek.

Ik neem aan dat we er nu van uit kunnen gaan dat het klopt Algoritme is hetzelfde gebleven bij mij, maar hij kan vast stukken sneller.

Conclusie durf ik nu wel te trekken, ~83% van de vectoren is uniek, maar door lage aantal bits vertekend dat. Mijn bruteforcer kan tot ongeveer ~12 wel resultaten neerzetten in acceptabele tijd, maar daarboven word het niet meer leuk om te wachten Als TS echt graag de score van 16 bits exact wil weten mag hij mijn programma wel een weekje laten draaien voor resultaten

[Soultaker]

Tabelletje tot en met 16 staat al in m'n vorige post hè.

(Berkend met dit programma, maar de OEIS aanpak is waarschijnlijk efficiënter, hoewel die volgens mij nog steeds wel O(4^diepte) ofzo is.)

[ Voor 61% gewijzigd door Soultaker op 09-02-2011 19:47 ]

[MLM]

De mijne is een naieve O(diepte^3) Teveel moeite om dat te refactoren als jij al uitkomsten hebt, ik kom op hetzelfde uit, dus het zal wel kloppen

[Soultaker]

O(diepte³) Dan zou diepte=16 een peuleschil moeten zijn (of je hebt gigantische overhead ) Ik denk dat je O(2^diepte³) bedoelt, oftewel O(2^3*diepte), oftewel O(8^diepte), maar dat geldt alleen als je in O(1) kunt factorizeren, wat me ook sterk lijkt.

Mijn aanpak is O(4^diepte*f) waarbij f de gemiddelde complexiteit van het Algoritme van Euclides is, wat vrij lastig te berekenen is, maar ongeveer op O(diepte) uitkomt.

[ Voor 7% gewijzigd door Soultaker op 09-02-2011 20:00 ]

[MLM]

Ik gebruik een lookuptable voor de factoren van elk getal in bereik (past makkelijk in de cache). Mijn inner loop is gewoon slecht, er zitten slecht predictable conditionals in die eruit gehaald kunnen worden (of in elk geval, gehoist naar die erboven)

Factorisatie is dus simpelweg zoeken in drie gesorteerde arrays van delers (gemiddeld voor diepte=16 heb je 9 delers). Ook dat doe ik naief op het moment, maar kan waarschijnlijk stukken sneller als ik wat edge-cases weg werk, waarbij O(1) niet ondenkbaar is.

Daarnaast, ik benut de symmetrie dat [1 0 0] en [0 1 0] en [0 0 1] tegelijk berekend kunnen worden niet, volgens mij kan je daarmee je problem area ongeveer met 2/3 verkleinen voor gevallen waarin R <> G <> B, wat verreweg de meeste zijn.

[ Voor 38% gewijzigd door MLM op 09-02-2011 20:43 ]

[Voutloos]

MLM schreef op woensdag 09 februari 2011 @ 20:18:
Daarnaast, ik benut de symmetrie dat \[1 0 0] en \[0 1 0] en \[0 0 1] tegelijk berekend kunnen worden niet.

Aan die tweak zat ik ook te denken, maar die is niet triviaal toe te passen in jouw algoritme...

Of kan je de binnenste loops tot de buitenste waarden begrenzen, zodat je (x,y,z) uitrekend met altijd x >= y >= z ?

edit:
Anders wacht ik heel lang met posten

MLM schreef op woensdag 09 februari 2011 @ 20:18:
volgens mij kan je daarmee je problem area ongeveer met 2/3 verkleinen voor gevallen waarin R <> G <> B, wat verreweg de meeste zijn.

Is het niet zelfs 5/6 voor die gevallen? Dus (uitkomst van die gevallen * 6 ) + (gevallen waar 2 getallen gelijk * 3) + 2.

[ Voor 32% gewijzigd door Voutloos op 09-02-2011 20:55 ]

[Soultaker]

For the record, de OEIS aanpak kan versimpeld worden tot:

C:

#include <stdio.h>

#define MAX_DEPTH 16

typedef long long ll;

int main()
{
    static ll memo[1<<MAX_DEPTH] = { 0, 7 };
    ll i, d;
    for (i = 2; i < (1<<MAX_DEPTH); ++i)
    {
        memo[i] = (i + 1)*(i + 1)*(i + 1) - i*i*i - 7;
        for (d = 2; d*d < i; ++d)
        {
            if (i%d == 0) memo[i] -= memo[d] + memo[i/d];
        }
        if (d*d == i) memo[i] -= memo[d];
    }
    for (d = 1; d <= MAX_DEPTH; ++d)
    {
        ll k = (1 << d) - 1, tot = (k + 1)*(k + 1)*(k + 1), cnt = tot;
        for (i = 1; i <= k; ++i) cnt -= (k/i - 1)*memo[i];
        printf("%2lld:  %15lld / %15lld = %.9f\n", d, cnt, tot, 1.0*cnt/tot);
    }
    return 0;
}

Dit is een O(2^3d/2) algoritme, dus relatief efficiënt. (Tot en met 16 bits runt in een fractie van een seconde.)

[Soultaker]

MLM schreef op woensdag 09 februari 2011 @ 20:18:
Ik gebruik een lookuptable voor de factoren van elk getal in bereik (past makkelijk in de cache).

Ok, zit je nog steeds met set intersection. Slimmer is om de gcd(x,y) voor x,y<=2^diepte te cachen, want de intersectie van de priemfactoren is leeg als gcd(x,y) == 1 (of dus 0, maar dan zijn beide getallen 0).

edit:
De ratio lijkt te convergeren naar 1/ζ(3); misschien kunnen we daar nog iets mee...

[ Voor 16% gewijzigd door Soultaker op 09-02-2011 21:16 ]

[barber]

Hangt het een en ander niet af van de kleurruimte die je gebruikt?

Ik heb 15 jaar geleden tijdens mijn studie nog wat geprogrammeerd aan het omzetten van RGB naar YUV (dus kennis kan roestig zijn ), waarbij Y de luminantie is en U en V de chrominanties. Maar dat was niet simpelweg de verhoudingen tussen RGB die de chrominantie bepaalden. Daar zat een simpele lineaire transformatie tussen.
(Even gezocht op wikipedia)


Of uitgeschreven:

code:

Y  = + 0.299R + 0.587G + 0.114B
U  = 0.492(B - Y)
   = - 0.147R - 0.289G + 0.436B
V  = 0.877(R - Y)
   = + 0.615R - 0.515G - 0.100B

Let op dat als R,G,B liggen in [0,1] dat Y[0,1] en U en V in [-0.5, 0.5] liggen.

Dus als RGB ieder 8 bits is, dan zijn er 8 bits voor luminantie en 2*8bits voor chrominantie.
Dus in het geval van bovenstaande kleurruimte is volgens mij per definitie dus 2/3 van de bits voor chrominantie en dus voor de kleur.

Ook als je de UV-vlak plot voor bijvoorbeeld Luminantie Y=0.5 dan krijg je zo'n mooi plaatje:

Dat lijken me allemaal unieke kleuren.

Maar ik ben geen expert in deze materie en heb alleen wat zitten klooien heel lang geleden om een jpeg encoder/decoder te schrijven in assembler.

Maar misschien kan het wel de juiste mensen hier triggeren om te zeggen dat ik complete onzin heb geschreven. ;-)

[Kid Jansen]

Het CIE 1931 xy chromaticity diagram geeft ook alleen unieke chrominanties weer, maar RGB geeft alleen een unieke chrominantie als een bepaalde combinate van R, G en B geen gemeenschappelijke deler heeft. Als dat wel het geval is, dan is de chrominantie hetzelfde als van de combinatie die je krijgt als je de getallen van de combinatie die je had deelt door die gemeenschappelijke deler.

Dit is overigens het CIE 1931 xy chromaticity diagram:

[Shagura]

Ja ik zat daar ook mee in mijn hoofd, maar ik vind het zelf nogal verwarrend. Daarnaast schaalt RGB ook helemaal niet lineair volgens mij dus vraag ik me af of je wel kan stellen dat dezelfde R, G en B verhoudingen ook altijd dezelfde chromaticiteit hebben.

[Kid Jansen]

RGB schaalt wel lineair in een paneel dacht ik, de signalen naar de monitor zijn echter gamma encoded / gamma compressed en ergens in de monitor vindt gamma decoding / gamma expansion plaats. De aansturing van de subpixels op het paneel ging dacht ik wel lineair.

[Klaasvaak]

Ik zat er nog is naar te kijken, ik heb nog geen wiskundige formule kunnen bouwen. Maar kwam bij 2 bits uit op 22 gevallen, inclusief zwart, waar de chromaticity gelijk zou zijn.

Toen in excel iets in elkaar geknutseld, wat tot 3 bits bruikbaar is. Hier kwamen 146 gevallen uit.

Het gaat bij de 2 bits versie waarschijnlijk om deze zes gevallen:
010, 011, 100, 101, 110, 111. (RGB in decimalen)
Die voldoen aan de voorwaarde:
(byte_rood < 0.5*(2^bits)) && (byte_geel < 0.5*(2^bits)) && (byte_blauw < 0.5*(2^bits))

[Shagura]

Kid Jansen schreef op woensdag 09 februari 2011 @ 22:06:
RGB schaalt wel lineair in een paneel dacht ik, de signalen naar de monitor zijn echter gamma encoded / gamma compressed en ergens in de monitor vindt gamma decoding / gamma expansion plaats. De aansturing van de subpixels op het paneel ging dacht ik wel lineair.

Ja je hebt gelijk het zou ook nergens op slaan als het niet lineair was in chromaticiteit. Alleen de luminance is niet lineair, maar dat maakt verder ook niet uit hiervoor.

Klaasvaak schreef op donderdag 10 februari 2011 @ 11:21:
Ik zat er nog is naar te kijken, ik heb nog geen wiskundige formule kunnen bouwen. Maar kwam bij 2 bits uit op 22 gevallen, inclusief zwart, waar de chromaticity gelijk zou zijn.

Toen in excel iets in elkaar geknutseld, wat tot 3 bits bruikbaar is. Hier kwamen 146 gevallen uit.

Het gaat bij de 2 bits versie waarschijnlijk om deze zes gevallen:
010, 011, 100, 101, 110, 111. (RGB in decimalen)
Die voldoen aan de voorwaarde:
(byte_rood < 0.5*(2^bits)) && (byte_geel < 0.5*(2^bits)) && (byte_blauw < 0.5*(2^bits))

Dit kan natuurlijk nooit kloppen. Als je een kleur hebt met 1 priemgetal die hoger is reken je die al niet mee. Daarnaast zijn natuurlijk nooit alle gevallen onder de half unieke combinaties. Is hier niks over te vinden verder? Het lijkt me een vrij algemeen probleem met permutaties eerlijk gezegd.

Zijn het niet gewoon alle permutaties met minstens 1 priemgetal (behalve 2 dan)?

[MLM]

<knip>
Zijn het niet gewoon alle permutaties met minstens 1 priemgetal (behalve 2 dan)?

Nee, bijvoorbeeld [9, 4, 10] heeft geen priemgetallen, maar is niet deelbaar
Wel kan je stellen dat alle permutaties met tenminste 1 priemgetal niet deelbaar zijn, maar dat is niet volledig

[ Voor 23% gewijzigd door MLM op 10-02-2011 14:17 ]

[Klaasvaak]

Wat ik bedoelde is dat bijvoorbeeld RGB 1,1,1 gelijke chromaticity met RGB 2,2,2 heeft. Maar RGB 1,1,1 wordt door het huidige algoritme niet opgepakt omdat deze enkel door 1 deelbaar is. Vandaar dus dat er gekeken moet worden of 2*R,2*G,2*B binnen het bereik valt dat mogelijk is met het aantal bits.

(2*R < (2^bits)) && (2*G < (2^bits)) && (2*B < (2^bits))

[Kid Jansen]

Soultaker schreef op woensdag 09 februari 2011 @ 21:02:
For the record, de OEIS aanpak kan versimpeld worden tot:

C:

#include <stdio.h>

#define MAX_DEPTH 16

typedef long long ll;

int main()
{
    static ll memo[1<<MAX_DEPTH] = { 0, 7 };
    ll i, d;
    for (i = 2; i < (1<<MAX_DEPTH); ++i)
    {
        memo[i] = (i + 1)*(i + 1)*(i + 1) - i*i*i - 7;
        for (d = 2; d*d < i; ++d)
        {
            if (i%d == 0) memo[i] -= memo[d] + memo[i/d];
        }
        if (d*d == i) memo[i] -= memo[d];
    }
    for (d = 1; d <= MAX_DEPTH; ++d)
    {
        ll k = (1 << d) - 1, tot = (k + 1)*(k + 1)*(k + 1), cnt = tot;
        for (i = 1; i <= k; ++i) cnt -= (k/i - 1)*memo[i];
        printf("%2lld:  %15lld / %15lld = %.9f\n", d, cnt, tot, 1.0*cnt/tot);
    }
    return 0;
}

Dit is een O(2^3d/2) algoritme, dus relatief efficiënt. (Tot en met 16 bits runt in een fractie van een seconde.)

Ik ben absoluut geen held in programmeren, dus snap niet helemaal wat de code precies doet, maar is het ook mogelijk om deze code aan te passen zodat hij alle unieke combinaties geeft?

Ik zou namelijk graag alle unieke combinaties voor 6 bit kleurdiepte (4 of 5 bit als dat te zwaar wordt) willen 3D-plotten in Matlab, om te zien wat voor patroon er ontstaat in de dichtheid van unieke combinaties.

[RobIII]

Moet je daar een topic uit 2011 voor uit de sloot trekken? Open gewoon even een topic volgens onze Quickstart a.u.b.